
����Ŀ�� ij��ѧ�Ļ������Ų��չ��һ������ƶ��˸�У���������������ָ������������ȼ���Ӧ��ϵ���±�������������������ָ�����ᳬ��300����
��������ָ�� |
|
|
|
|
|
|
���������ȼ� |
|
|
��Ⱦ |
��Ⱦ |
��Ⱦ |
|
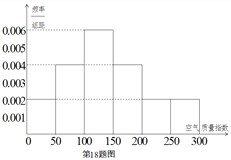
�����Ž���У����2016��100��Ŀ�������ָ�����������Ϊ���������Ƶ�Ƶ�ʷֲ�ֱ��ͼ����ͼ���Ѹ�ֱ��ͼ����Ƶ�ʹ���Ϊ������
�����������2017�꣨��365����㣩ȫ�������������������(δ��һ�찴һ�����)��
�������÷ֲ�����ķ�������ȡ10�죬���������ָ���ڣ�0��50]��(50��100]��(100��150]�������и�Ӧ��ȡ���죿
��������֪���������ȼ�Ϊ1��ʱ����Ҫ�������������������ȼ�Ϊ2��ʱÿ���辻�������ķ���Ϊ2000Ԫ�����������ȼ�Ϊ3��ʱÿ���辻�������ķ���Ϊ4000Ԫ�������������������£��ӿ�������ָ����![]() �������������ȡ��������������ľ��������ܷ���Ϊ4000Ԫ�ĸ�����
�������������ȡ��������������ľ��������ܷ���Ϊ4000Ԫ�ĸ�����
���𰸡�������110����������Ӧ��ȡ1��2��3���������� ![]() ��
��
���������������������������ֱ��ͼ�ɵù���2017�꣨��365����㣩ȫ���������������Ƶ�ʣ��Ӷ��ɵý��������������ÿ�������ָ���ڣ�0��50]��(50��100]��(100��150]�������ı������Ӷ����ݷֲ���������ɵý�������������оٳ���������ָ���� �������������ȡ���칲��![]() �֣����������Ĺ���
�֣����������Ĺ���![]() �֣����ݹŵ�����ʹ�ʽ�ɵý��.
�֣����ݹŵ�����ʹ�ʽ�ɵý��.
�����������������ֱ��ͼ�ɹ���2017�꣨��365����㣩ȫ�������������������Ϊ
![]() ���죩��
���죩��
��������������ָ���ڣ�0��50]��(50��100]��(100��150]�������и�Ӧ
��ȡ1��2��3����
�������������ָ���ڣ�0��50]��һ��ΪA����������ָ���ڣ�50��100]������Ϊb��c��
��������ָ���ڣ�100��150]������Ϊ1��2��3����������������ȡ��������п��ܽ��Ϊ��Ab������Ac������A1������A2������A3������bc������b1������b2������b3������c1������c2������c3������12������13������23��.��15��.
����������ľ��������ܷ���Ϊ4000Ԫ�Ŀ��ܽ��Ϊ��A1������A2������A3������bc��.
P(������ľ��������ܷ���Ϊ4000Ԫ)= ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ��������30�ˣ�������90�ˣ�������60�ˣ�Ϊ�˵������ǵ����彡��״�������÷ֲ�����ķ����������м��ȡһ������Ϊ36����������Ӧ��ȡ�����˵������ǣ� ��
A.5
B.6
C.7
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
(I)����![]() �ĵ������䣻
�ĵ������䣻
(II)��![]() ����֪����
����֪����![]() ��
��![]() ������������
������������
(1)�о�����![]() �����ĸ�����
�����ĸ�����
(ii)��ʵ��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1���� ![]() ʱ���ⲻ��ʽf��x����x+10��
ʱ���ⲻ��ʽf��x����x+10��
��2������x�IJ���ʽf��x����a��R�Ϻ��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4:����ϵ���������
��ֱ������ϵ![]() �У�Բ
�У�Բ![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������OΪ���㣬
Ϊ����������OΪ���㣬 ![]() ��ķǸ�����Ϊ���Ὠ��������ϵ.
��ķǸ�����Ϊ���Ὠ��������ϵ.
��������Բ![]() ����ͨ���̣�
����ͨ���̣�
������ֱ��![]() �ļ����귽����
�ļ����귽����![]() ������
������![]() ��ԲC�Ľ���Ϊ
��ԲC�Ľ���Ϊ![]() ����ֱ��
����ֱ��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() �����߶�
�����߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�Ŀռ��ı���ABCD�У�E��F��G��H�ֱ���AB��BC��CD��AD���е㣬��ͼ�й��ж��ٶ�����ƽ�й�ϵ���� �� 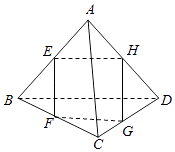
A.2��
B.4��
C.6��
D.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
������![]() ������
������![]() �ļ�ֵ��
�ļ�ֵ��
������![]() ,
,![]() ,
,![]() ,ʹ��
,ʹ��![]() ��
��![]() ������ʵ��
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ڶԸ���ѧ����4��������ѧ���в��Ե�����ͳ����ʾ��ȫ��10000��ѧ���ijɼ�������̬�ֲ�![]() ���ִӼ�У100�����ϣ���100�֣���200���Ծ�����ϵͳ�����ķ�����ȡ��20���Ծ���������ͳ�����£�
���ִӼ�У100�����ϣ���100�֣���200���Ծ�����ϵͳ�����ķ�����ȡ��20���Ծ���������ͳ�����£�

��ע�������Ծ����![]() ��
��
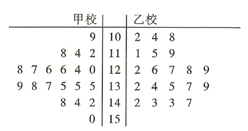
��1���г������Ծ��÷�Ϊ126�ֵ��Ծ���ţ�д���������ݣ���
��2�������ִ���У��Ҳ��ϵͳ�����ķ�����ȡ��20���Ծ�����������У��40���Ծ��ĵ÷������˾�Ҷͼ����ͼ6������ͨ����Ҷͼ�Ƚ���Уѧ���ɼ���ƽ���ּ���ɢ�̶ȣ�����Ҫ����������ֵ���������ۼ��ɣ���
��3���ڵڣ�2���ʵ�ǰ���£��Ӽ�����У��40��ѧ���У��ӳɼ���140�����ϣ���140�֣���ѧ���������ȡ3�ˣ���3����ȫ��ǰ15����������Ϊ![]() ����
����![]() �ķֲ��к�����.
�ķֲ��к�����.
���������������![]() ������̬�ֲ�
������̬�ֲ�![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У�����Ϊ��ʾ��������ƽ��������������һ������ǣ� ��
A.![]() =��0��0��
=��0��0�� ![]() =��1����2��
=��1����2��
B.![]() =����1��2��
=����1��2�� ![]() =��3��7��
=��3��7��
C.![]() =��3��5��
=��3��5�� ![]() =��6��10��
=��6��10��
D.![]() =��2����3��
=��2����3�� ![]() =��
=�� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com