
【题目】设![]() ,在集合
,在集合![]() 的所有元素个数为2的子集中,把每个子集的较大元素相加和记为a,较小元素之和记为b.
的所有元素个数为2的子集中,把每个子集的较大元素相加和记为a,较小元素之和记为b.
(1)当n=3时,求a, b的值;
(2)当n=4时,求集合![]() 的所有3个元素子集
的所有3个元素子集![]() 中所有元素之和
中所有元素之和![]() ;
;
(3)对任意的![]() ,
,![]() 是否为定值?若是定值,请给出证明并求出这个定值;若不是,请说明理由.
是否为定值?若是定值,请给出证明并求出这个定值;若不是,请说明理由.
【答案】(1)![]() ;
;![]() (2)
(2)![]() (3)见证明
(3)见证明
【解析】
(1)根据题干所给的概念可得到相应的参数值;(2)含有元素1的子集有![]() 个,同理含有2,3,4的子集也有
个,同理含有2,3,4的子集也有![]() 个,元素之和为
个,元素之和为![]() ;(3)根据题意分析得到a和b的表达式,再由组合数的公式得到结果.
;(3)根据题意分析得到a和b的表达式,再由组合数的公式得到结果.
(1)集合![]() 的所有2元子集为
的所有2元子集为![]() ,
,![]() ,
,![]() ,
,
较大元素分别为2,3,3,所以![]() ;
;
较小元素分别为1,1,2,所以![]() .
.
(2)含有元素1的子集有![]() 个,同理含有2,3,4的子集也有
个,同理含有2,3,4的子集也有![]() 个
个
于是所求元素之和为![]()
(3)![]() 是为定值,定值为
是为定值,定值为![]()
当n≥4,n∈N*,当较小元素为1时,这样的2元素集合有![]() 个,较小元素为2时,这样的2元素集合为
个,较小元素为2时,这样的2元素集合为![]() ,依次类推,较小元素为n-1的集合个数为1个,
,依次类推,较小元素为n-1的集合个数为1个,
![]()
同上,当较大元素为2时,这样的2元素集合有1个,较大元素为3的2元素集合为2个,依此类推得到较大元素为n时,集合个数为![]() 个,进而得到:
个,进而得到:
![]()
![]()
![]()
![]()
![]()
所以![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒

A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山西省2021年高考将实施新的高考改革方案.考生的高考总成绩将由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、历史、政治、地理6科中选择3门作为选考科目,语、数、外三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分。根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.等级考试科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.等级考试科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到![]()
![]() 八个分数区间,得到考生的等级成绩。举例说明1:甲同学化学学科原始分为65分,化学学科
八个分数区间,得到考生的等级成绩。举例说明1:甲同学化学学科原始分为65分,化学学科![]() 等级的原始分分布区间为
等级的原始分分布区间为![]() ,则该同学化学学科的原始成绩属
,则该同学化学学科的原始成绩属![]() 等级,而
等级,而![]() 等级的转换分区间为
等级的转换分区间为![]() 那么,甲同学化学学科的转换分为:设甲同学化学科的转换等级分为
那么,甲同学化学学科的转换分为:设甲同学化学科的转换等级分为![]() ,求得
,求得![]() .四舍五入后甲同学化学学科赋分成绩为66分。举例说明2:乙同学化学学科原始分为69分,化学学科
.四舍五入后甲同学化学学科赋分成绩为66分。举例说明2:乙同学化学学科原始分为69分,化学学科![]() 等级的原始分分布区间为
等级的原始分分布区间为![]() 则该同学化学学科的原始成绩属
则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为
等级的转换分区间为![]() 这时不用公式,乙同学化学学科赋分成绩直接取下端点70分。现有复兴中学高一年级共3000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布
这时不用公式,乙同学化学学科赋分成绩直接取下端点70分。现有复兴中学高一年级共3000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布![]() 。且等级为
。且等级为![]() 所在原始分分布区间为
所在原始分分布区间为![]() ,且等级为
,且等级为![]() 所在原始分分布区间为
所在原始分分布区间为![]() ,且等级为
,且等级为![]() 所在原始分分布区间为
所在原始分分布区间为![]()
(1)若小明同学在这次考试中物理原始分为84分,小红同学在这次考试中物理原始分为72分,求小明和小红的物理学科赋分成绩;(精确到整数).
(2)若以复兴中学此次考试频率为依据,在学校随机抽取4人,记![]() 这4人中物理原始成绩在区间
这4人中物理原始成绩在区间![]() 的人数,求
的人数,求![]() 的数学期望和方差.(精确到小数点后三位数).
的数学期望和方差.(精确到小数点后三位数).
附:若随机变量满足正态分布,给出以下数据![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人们的生活水平也同步上升,许许多多的家庭对于资金的管理都有不同的方式。最新调查表明,人们对于投资理财的兴趣逐步提高。某投资理财公司做了大量的数据调查,调查显示两种产品投资收益如下:
①投资![]() 产品的收益与投资额的算术平方根成正比;
产品的收益与投资额的算术平方根成正比;
②投资![]() 产品的收益与投资额成正比.
产品的收益与投资额成正比.
公司提供了投资1万元时两种产品的收益,分别是0.4万元和0.2万元。
(1) 分别求出![]() 产品的收益
产品的收益![]() 、
、![]() 产品的收益
产品的收益![]() 与投资额
与投资额![]() 的函数关系式;
的函数关系式;
(2) 假如现在你有10万元的资金全部用于投资理财,你该如何分配资金,才能让你的收益最大?最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究塞卡病毒(Zika virus)某种疫苗的过程中,为了研究小白鼠连续接种该种疫苗后出现![]() 症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现
症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现![]() 症状的概率为
症状的概率为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若出现![]() 症状即停止试验,求试验至多持续一个接种周期的概率;
症状即停止试验,求试验至多持续一个接种周期的概率;
(2)若在一个接种周期内出现2次货3次![]() 症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为
症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对食堂伙食的满意程度,组织学生给食堂打分(分数为整数,满分100分),从中随机抽取一个容量为![]() 的样本,发现所有数据均在
的样本,发现所有数据均在![]() 内.现将这些分数分成以下
内.现将这些分数分成以下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
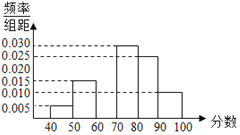
(1)算出第三组![]() 的频数,并补全频率分布直方图;
的频数,并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数和平均数,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com