分析:(1)根据点C到点F的距离等于它到l
1的距离,依据抛物线的定义可知点C的轨迹是以F为焦点,l
1为准线的抛物线,进而求得其轨迹方程.
(2)设出直线l
2的方程与抛物线方程联立消去y,设出P,Q的坐标,根据韦达定理表示出x
1+x
2和x
1x
2的表达式,进而可得点R的坐标,表示出
•,根据均值不等式求得其最小值.
解答:解:(1)由题设点C到点F的距离等于它到l
1的距离,
∴点C的轨迹是以F为焦点,l
1为准线的抛物线
∴所求轨迹的方程为x
2=4y
(2)由题意直线l
2的方程为y=kx+1,
与抛物线方程联立消去y得x
2-4kx-4=0.
记P(x
1,y
1),Q(x
2,y
2),则x
1+x
2=4k,x
1x
2=-4.
因为直线PQ的斜率k≠0,易得点R的坐标为
(-,-1)•=(x1+,y1+1)•(x2+,y2+1)=
(x1+)(x2+)+(kx1+2)(kx2+2)=
(1+k2)x1x2+(+2k)(x1+x2)++4=
-4(1+k2)+4k(+2k)++4=
4(k2+)+8,
∵
k2+≥2,当且仅当k
2=1时取到等号.
•≥4×2+8=16,即•的最小值为16
点评:本题主要考查了直线与圆锥曲线的关系.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法,

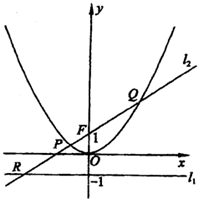 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.

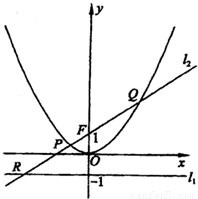 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.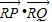 的最小值.
的最小值.