
【题目】在1,2之间插入n个正数a1 , a2 , …,an , 使这n+2个数成等比数列,则a1a2a3…an= .
科目:高中数学 来源: 题型:
【题目】对于向量a,b,e及实数x,y,x1,x2,![]() ,给出下列四个条件:
,给出下列四个条件:
①![]() 且
且![]() ; ②
; ②![]()
③![]() 且
且![]() 唯一; ④
唯一; ④![]()
其中能使a与b共线的是 ( )
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 且函数y=f(x)﹣x恰有3个不同的零点,则实数a的取值范围是( )
且函数y=f(x)﹣x恰有3个不同的零点,则实数a的取值范围是( )
A.(0,+∞)
B.[﹣1,0)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的反函数为
的反函数为 ![]() ,等比数列{an}的公比为2,若
,等比数列{an}的公比为2,若 ![]() ,则
,则 ![]() =( )
=( )
A.21004×2016 ![]()
B.21005×2015
C.21005×2016
D.21008×2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,2012年春节,摄影爱好者![]() 在某公园
在某公园![]() 处,发现正前方
处,发现正前方![]() 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端![]() 的仰角和立柱底部
的仰角和立柱底部![]() 的俯角均为
的俯角均为![]() ,设
,设![]() 的眼睛距地面的距离
的眼睛距地面的距离![]() 米.
米.
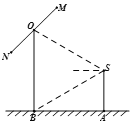
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆![]() 绕其中点
绕其中点![]() 在
在![]() 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 向
向![]() 轴作垂线段
轴作垂线段![]() ,垂足为
,垂足为![]() ,当点
,当点![]() 在圆上运动时,线段
在圆上运动时,线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() (0,-2)作直线
(0,-2)作直线![]() 与
与![]() 交于
交于![]() 两点,(O为原点),求三角形
两点,(O为原点),求三角形![]() 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=(1﹣m)lnx+![]() +nx(m,n是常数).
+nx(m,n是常数).
(1)若m=0,且f(x)在(1,2)上单调递减,求n的取值范围;
(2)若m>0,且n=﹣1,求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:

已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.

参考公式:![]() ,其中
,其中 ![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com