
| A. | $[2kπ-\frac{π}{4},2kπ+\frac{π}{4})\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | B. | $[2kπ-\frac{5π}{4},2kπ-\frac{π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | ||
| C. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | D. | $(2kπ-\frac{3π}{4},2kπ-\frac{π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ |
分析 由复合函数的单调性可知,内函数满足函数值大于0的减区间即为原函数的减区间,可得2kπ≤x+$\frac{π}{4}$<2kπ$+\frac{π}{2}$,k∈Z,求得x的范围得答案.
解答 解:令t=$cos(x+\frac{π}{4})$,
∵外函数y=log2t为定义域内的增函数,
∴内函数满足函数值大于0的减区间即为原函数的减区间,
则由2kπ≤x+$\frac{π}{4}$<2kπ$+\frac{π}{2}$,k∈Z,
得$2kπ-\frac{π}{4}≤x<2kπ+\frac{π}{4}$,k∈Z.
∴函数$y={log_2}cos(x+\frac{π}{4})$的单调减区间为[$2kπ-\frac{π}{4},2kπ+\frac{π}{4}$),k∈Z.
故选:A.
点评 本题主要考查了复合函数的单调性以及单调区间的求法.对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{25}$ | B. | $-\frac{2}{25}$ | C. | $-\frac{23}{25}$ | D. | $\frac{2}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
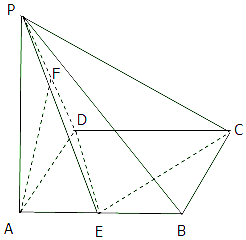 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=3,F是PD的中点,E是线段AB上的点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=3,F是PD的中点,E是线段AB上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com