
【题目】如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E. 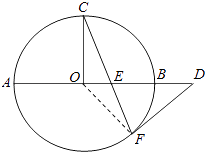
(1)求证:DE2=DBDA;
(2)若DB=2,DF=4,试求CE的长.
【答案】
(1)证明:连接OF.
因为DF切⊙O于F,所以∠OFD=90°.
所以∠OFC+∠CFD=90°.
因为OC=OF,所以∠OCF=∠OFC.
因为CO⊥AB于O,所以∠OCF+∠CEO=90°.
所以∠CFD=∠CEO=∠DEF,所以DF=DE.
因为DF是⊙O的切线,所以DF2=DBDA.
所以DE2=DBDA
(2)解:∵DF2=DBDA,DB=2,DF=4.
∴DA=8,从而AB=6,则OC=3.
又由(1)可知,DE=DF=4,∴BE=2,OE=1.
从而 在Rt△COE中, ![]()
【解析】(1)连接OF,利用切线的性质及角之间的互余关系得到DF=DE,再结合切割线定理证明DE2=DBDA,即可求出DE.(2)求出BE=2,OE=1,利用勾股定理求CE的长.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(.(12分)在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为调查高中生选修课的选修倾向与性别关系,随机抽取50名学生,得到如表的数据表:
倾向“平面几何选讲” | 倾向“坐标系与参数方程” | 倾向“不等式选讲” | 合计 | |
男生 | 16 | 4 | 6 | 26 |
女生 | 4 | 8 | 12 | 24 |
合计 | 20 | 12 | 18 | 50 |
(1)根据表中提供的数据,选择可直观判断“选课倾向与性别有关系”的两种,作为选课倾向的变量的取值,并分析哪两种选择倾向与性别有关系的把握大;
附:K2= ![]() .
.
P(k2≤k0) | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(2)在抽取的50名学生中,按照分层抽样的方法,从倾向“平面几何选讲”与倾向“坐标系与参数方程”的学生中抽取8人进行问卷.若从这8人中任选3人,记倾向“平面几何选讲”的人数减去与倾向“坐标系与参数方程”的人数的差为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(cosβ)
D.f(sinα)>f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)的表达式为f(x)= ![]() (c≠0),则函数f(x)的图象的对称中心为(﹣
(c≠0),则函数f(x)的图象的对称中心为(﹣ ![]() ,
, ![]() ),现已知函数f(x)=
),现已知函数f(x)= ![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f( ![]() )(n∈N),则此数列前2017项的和为 .
)(n∈N),则此数列前2017项的和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com