
【题目】已知圆![]() 与直线
与直线![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.
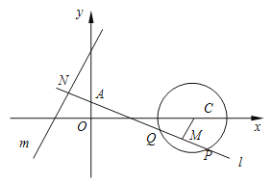
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() . 探索
. 探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像经过点
的图像经过点![]() ,且
,且![]() 的相邻两个零点的距离为
的相邻两个零点的距离为![]() ,为得到
,为得到![]() 的图像,可将
的图像,可将![]() 图像上所有点( )
图像上所有点( )
A.先向右平移![]() 个单位,再将所得图像上所有点的横坐标缩短为原来的
个单位,再将所得图像上所有点的横坐标缩短为原来的![]() ,纵坐标不变
,纵坐标不变
B.先向左平移![]() 个单位,再将所得图像上所有点的横坐标缩短为原来的
个单位,再将所得图像上所有点的横坐标缩短为原来的![]() ,纵坐标不变
,纵坐标不变
C.先向左平移![]() 个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
D.先向右平移![]() 个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。

(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,k≠0,k∈R.
,k≠0,k∈R.
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)已知f(x)在(﹣∞,0]上单调递减,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曙光中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出![]() 名学生,将其成绩(均为整数)分成六段
名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,
,![]() ,
,![]() 后画出如下部分频率分布直方图,则第四小组的频率为_______,从成绩是
后画出如下部分频率分布直方图,则第四小组的频率为_______,从成绩是![]() 和
和![]() 的学生中选两人,他们在同一分数段的概率_______.
的学生中选两人,他们在同一分数段的概率_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() ,平面
,平面![]() 截此三棱柱,分别与
截此三棱柱,分别与![]() ,
, ![]() ,
, ![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且直线
,且直线![]() 平面
平面![]() .有下列三个命题:①四边形
.有下列三个命题:①四边形![]() 是平行四边形;②平面
是平行四边形;②平面![]() 平面
平面![]() ;③若三棱柱
;③若三棱柱![]() 是直棱柱,则平面
是直棱柱,则平面![]() 平面
平面![]() .其中正确的命题为( )
.其中正确的命题为( )
A. ①② B. ①③ C. ①②③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com