
 (1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;
(1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| 7 |
| 9 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| π |
| 2 |
| 1 |
| 3 |
| 1-cos2β |
2
| ||
| 3 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 7 |
| 9 |
| 1-sin2(α+β) |
4
| ||
| 9 |
2
| ||
| 3 |
| 22 |
| 9 |


科目:高中数学 来源: 题型:
| 1 |
| x2+1 |
| 1 |
| x |

查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
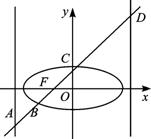
素材2:设f(m)=||AB|-|CD||.
试根据上述素材构建一个问题,然后再解答.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省沭阳县高一下学期期中调研测试数学试卷(解析版) 题型:解答题
(1)如图,已知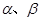 是坐标平面内的任意两个角,且
是坐标平面内的任意两个角,且 ,证明两角差的余弦公式:
,证明两角差的余弦公式: ;
;
(2)已知 ,且
,且 ,
, ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com