
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)若![]() ,且对任意的
,且对任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)0;(2) ![]() .
.
【解析】试题分析:(1)求出函数的导数,得到函数的单调区间,求出函数的最大值即可;
(2)令(x)=f(x)+1,根据函数的单调性分别求出φ(x)的最小值和g(x)的最大值,得到关于m的不等式,解出即可.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
(2)令![]() ,因为“对任意的
,因为“对任意的![]() ,
, ![]() 恒成立”,
恒成立”,
所以对任意的![]() ,
, ![]() 成立,由于
成立,由于![]() ,
,
当![]() 时,对
时,对![]() 有
有![]() ,从而函数
,从而函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,显然不满足
,显然不满足![]() ,
,
当![]() 时,令
时,令![]() 得
得![]() ,
, ![]() ,
,
①当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,只需
,只需![]() ,得
,得![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,
, ![]() 单调递增,在
单调递增,在![]() 上
上![]() ,
, ![]() 单调递减,所以
单调递减,所以![]() ,只需
,只需![]() ,得
,得![]() ,所以
,所以![]() .
.
③当![]() ,即
,即![]() 时,显然在
时,显然在![]() 上
上![]() ,
, ![]() 单调递增,所以
单调递增,所以![]() ,
, ![]() 不成立.
不成立.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=ax﹣lnx,x∈(0,e],其中e是自然常数,a∈R.
(1)当a=1时,求f(x)的单调区间和极值;
(2)是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
(3)证明:(1﹣ ![]() )(
)( ![]() )(
)( ![]() ﹣
﹣ ![]() )…(
)…( ![]() ﹣
﹣ ![]() )<e3(3﹣n) .
)<e3(3﹣n) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则14分钟后P点距地面的高度是米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某正弦交流电的电压v(单位V)随时间t(单位:s)变化的函数关系是v=120 ![]() sin(100πt﹣
sin(100πt﹣ ![]() ),t∈[0,+∞).
),t∈[0,+∞).
(1)求该正弦交流电电压v的周期、频率、振幅;
(2)若加在霓虹灯管两端电压大于84V时灯管才发光,求在半个周期内霓虹灯管点亮的时间?( 取 ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
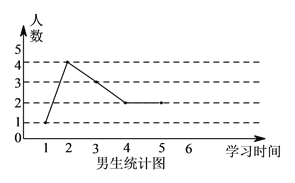
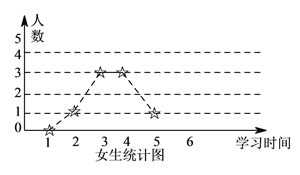
(I)已知该校有![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于![]() 小时的学生中选取
小时的学生中选取![]() 人,设选到的男生人数为
人,设选到的男生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差![]() 与女生学习时间方差
与女生学习时间方差![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,椭圆的离心率为
上的两点,椭圆的离心率为![]() ,短轴长为2,已知向量
,短轴长为2,已知向量![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆的焦点
过椭圆的焦点![]() ,(
,( ![]() 为半焦距),求直线
为半焦距),求直线![]() 的斜率
的斜率![]() 的值;
的值;
(2)试问: ![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com