练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．过点P（1，2），并且在两坐标轴上的截距相等的直线方程是（　　）
    A．x+y-3=0或x-2y=0B．x+y-3=0或2x-y=0
    C．x-y+1=0或x+y-3=0D．x-y+1=0或2x-y=0

    分析 当直线经过原点时，可得直线方程：y=2x．当直线不经过原点时，可设直线方程为：x+y=a，把点（1，2）代入即可得出．

    解答 解：当直线经过原点时，可得直线方程：y=2x．
    当直线不经过原点时，可设直线方程为：x+y=a，则a=1+2=3．可得直线方程为：x+y=3．
    综上可得，直线方程为：x+y+3=0或2x-y=0．
    故选：B．

    点评 本题考查了直线方程、截距式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．设ω＞0，将函数f（x）=$\sqrt{2}$cosωx的图象向左平移$\frac{π}{2}$个单位，若所得的图象与原图象重合，则正数ω的最小值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知圆M：（x-2）2+（y-2）2=2，圆N：x2+（y-8）2=40，经过原点的两直线l1，l2满足l1⊥l2，且l1交圆M于不同两点A，B，l2交圆N于不同两点C，D，记l1的斜率为k．
    （1）求k的取值范围；
    （2）若四边形ABCD为梯形，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

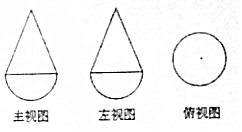    9．已知一个几何体是由上下两部分组成的合体，其三视图如图，若图中圆的半径为1，等腰三角形的腰长为$\sqrt{5}$，则该几何体的体积是（　　）
    A．$\frac{4π}{3}$B．2πC．$\frac{8π}{3}$D．$\frac{10π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

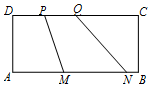    16．如图，矩形ABCD中，AB=2AD=4，MN=2PQ=2，向该矩形内随机投一质点，则质点落在四边形MNQP内的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{3}{8}$C．$\frac{2}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．log240-log25=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

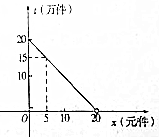    13．2016年9月，第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行，在会展期间某展销商销售一种商品，根据市场调查，每件商品售价x（元）与销量t（万元）之间的函数关系如图所示，又知供货价格与销量呈反比，比例系数为20．（注：每件产品利润=售价-供货价格）
    （1）求售价15元时的销量及此时的供货价格；
    （2）当销售价格为多少时总利润最大，并求出最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知命题p：?x∈[1，$\sqrt{2}$]，x2-a≥0，命题q：?x0∈R，$\frac{1}{4}$x02-ax0+2-a=0，若命题“p∧q”为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若函数f（x）=$\frac{sinx}{x+1}$，则f′（0）等于（　　）
    A．1B．0C．-1D．-2

    查看答案和解析>>

    同步练习册答案