
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
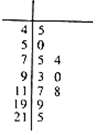 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
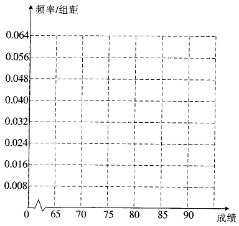 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | 8 | 0.32 |
| (80,85] | 7 | 0.28 |
| (85,90] | 2 | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
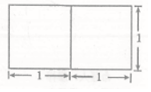 一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )
一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )| A. | $\frac{19}{6}$ | B. | $\frac{38}{3}$ | C. | $\frac{57}{8}$ | D. | $\frac{19}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com