
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由数列的定义及极限的定义,举反例即可.
解答 解:①若$\underset{lim}{n→∞}$an存在,不妨设$\underset{lim}{n→∞}$an=A,则$\underset{lim}{n→∞}$an2=A2,故成立;
②不妨设an=(-1)n,故$\underset{lim}{n→∞}$|an|存在,$\underset{lim}{n→∞}$an不存在;
③若$\underset{lim}{n→∞}$an存在,不妨设$\underset{lim}{n→∞}$an=A,当A=-1时,$\underset{lim}{n→∞}$$\frac{{a}_{n}}{{a}_{n}+1}$不存在.
④若$\underset{lim}{n→∞}$(an-bn)=A,$\underset{lim}{n→∞}$(an+bn)=B,则$\underset{lim}{n→∞}$an=$\frac{A+B}{2}$,$\underset{lim}{n→∞}$bn=$\frac{B-A}{2}$;
故选:C.
点评 本题考查了极限的定义及数列的定义的应用.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
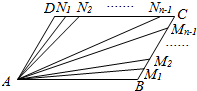 如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )
如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a-1)f(1)+(2-a)f(2) | B. | (2-a)f(1)+(a-1)f(2) | C. | (2-a)f(1)+(1-a)f(2) | D. | (1-a)f(1)+(2-a)f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,4] | B. | (-4,4) | C. | [-4,0)∪(0,4] | D. | (-∞,4)∪(4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com