
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,则在圆
,则在圆![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,使得
,使得![]() ,
,![]() ?若存在,请求出
?若存在,请求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() 是以
是以![]() 为焦点,
为焦点,![]() 为准线的抛物线(2)存在;
为准线的抛物线(2)存在;![]()
【解析】
(1)根据题意可得![]() ,再根据抛物线的定义即可求出曲线
,再根据抛物线的定义即可求出曲线![]() 的方程.
的方程.
(2)将直线![]() 与曲线
与曲线![]() :
:![]() 联立,由直线
联立,由直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,利用韦达定理可得
,利用韦达定理可得![]() ,从而求出
,从而求出![]() 的中垂线方程,由
的中垂线方程,由![]() ,
,![]() ,可得
,可得![]() 的中垂线与圆
的中垂线与圆![]() 交于两点
交于两点![]() 、
、![]() ,利用点到直线的距离公式使圆心到直线的距离小于半径即可求解.
,利用点到直线的距离公式使圆心到直线的距离小于半径即可求解.
(1)由题意,得![]() ,则动点
,则动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,
![]() 为准线的抛物线,所以点
为准线的抛物线,所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由![]() 得
得![]() .
.
由直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,
,
得![]() ,解得
,解得![]() .
.
由韦达定理,得![]() .
.
设![]() 的中点为
的中点为![]() ,
,
则![]() ,
,![]() ,
,
即![]() ,
,
所以![]() 的中垂线方程为
的中垂线方程为![]() ,即
,即![]() ,
,
由![]() ,
,![]() ,得
,得![]() 的中垂线与圆
的中垂线与圆![]() 交于两点
交于两点![]() 、
、![]() ,
,
所以![]() ,解得
,解得![]() .
.
由①和②,得![]() .
.
综上,当![]() 时,圆
时,圆![]() 上存在两点
上存在两点![]() 、
、![]() ,使得
,使得![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两位战士参加射击比赛训练.从若干次预赛成绩中随机抽取8次,记录如下:
甲82 81 79 78 95 88 93 84
乙92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据,并分别求两组数据的中位数;
(2)现要从中选派一人参加射击比赛,从统计学的角度考虑,你认为选派哪位战士参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 和圆
和圆![]() 均内切.
均内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于
且垂直于![]() 的直线交轨迹
的直线交轨迹![]() 于两点
于两点![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为A,右焦点为F,O是坐标原点,
的上顶点为A,右焦点为F,O是坐标原点,![]() 是等腰直角三角形,且周长为
是等腰直角三角形,且周长为![]() .
.
(1)求椭圆的方程;
(2)若直线l与AF垂直,且交椭圆于B,C两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是全球最大的口罩生产国,在2020年3月份,我国每日口罩产量超一亿只,已基本满足国内人民的需求,但随着疫情在全球范围扩散,境外口罩需求量激增,世界卫生组织公开呼吁扩大口罩产能常见的口罩有![]() 和
和![]() (分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产
(分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产![]() 和
和![]() 两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
总分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
(1)试分别估计两种口罩的合格率;
(2)假设生产一个![]() 口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个
口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个![]() 口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
①设![]() 为生产一个
为生产一个![]() 口罩和生产一个
口罩和生产一个![]() 口罩所得利润的和,求随机变量
口罩所得利润的和,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②求生产4个![]() 口罩所得的利润不少于8元的概率
口罩所得的利润不少于8元的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
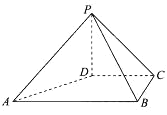
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com