(1)证明∵函数定义域为R,其定义域关于原点对称.
∵f(x+y)-f(x)+f(y),令y=-x,∴f(0)=f(x)+f(-x).令x=y=0,
∴f(0)-f(0)+f(0),得f(0)=0.∴f(x)+f(-x)=0,得f(-x)=-f(x),
∴f(x)为奇函数.
(2)解 方法一 设x,y∈R
+,∵f(x+y)=f(x)+f(y),
∴f(x+y)-f(x)=f(y).∵x∈R
+,f(x)<0,
∴f(x+y)-f(x)<0,∴f(x+y)<f(x).
∵x+y>x,∴f(x)在(0,+∞)上是减函数.又∵f(x)为奇函数,f(0)=0,
∴f(x)在(-∞,+∞)上是减函数.∴f(-2)为最大值,f(6)为最小值.
∵f(1)=-
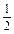
,∴f(-2)=-f(2)=-2f(1)=1,
f(6)=2f(3)=2[f(1)+f(2)]=-3.
∴所求f(x)在区间[-2,6]上的最大值为1,最小值为-3.
方法二 设x
1<x
2,且x
1,x
2∈R.
则f(x
2-x
1)=f[x
2+(-x
1)]=f(x
2)+f(-x
1)=f(x
2)-f(x
1).
∵x
2-x
1>0,∴f(x
2-x
1)<0.∴f(x
2)-f(x
1)<0.即f(x)在R上单调递减.
∴f(-2)为最大值,f(6)为最小值.∵f(1)=-
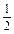
,
∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.
∴所求f(x)在区间[-2,6]上的最大值为1,最小值为-3.

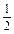 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.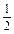 ,∴f(-2)=-f(2)=-2f(1)=1,
,∴f(-2)=-f(2)=-2f(1)=1,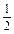 ,
, 
