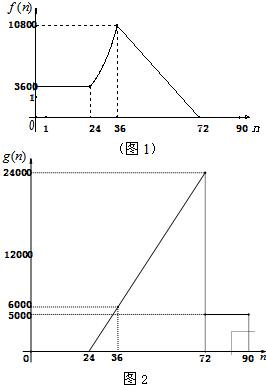如图2-3-10,在△OAB中,若OA =OB =2a,⊙O的半径r =a.问:AB与⊙O相切.相交.相离时,∠AOB的取值范围如何?图2-3-10 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

如图2-3-10,在△OAB中,若OA =OB =2a,⊙O的半径r =a.问:AB与⊙O相切、相交、相离时,∠AOB的取值范围如何?

图2-3-10

思路分析:先作出O到AB的距离OC,根据AB与⊙O的不同位置关系确定OC的取值范围,从而再确定∠AOB的取值范围.

解:过O作OC⊥AB,垂足为C,?

(1)当AB与⊙O相切时,OC =r =a,此时cos∠AOC = =,?

∴∠AOC=60°.?

又∵OA =OB,∴OC平分∠AOB.?

∴∠AOB =120°.?

(2)当AB与⊙O相交时,OC ＜r =a,此时cos∠AOC ＜,?

∴60°＜∠AOC＜90°.?

∴120°＜∠AOB＜180°.?

(3)当AB与⊙O相离时,OC ＞r,此时cos∠AOC ＞,?

∴0°＜∠AOC ＜60°.∴0°＜∠AOB＜120°.

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

2010年上海世博会组委会为保证游客参观的顺利进行，对每天在各时间段进入园区和离开园区的人数作了一个模拟预测．为了方便起见，以10分钟为一个计算单位，上午9点10分作为第一个计算人数的时间，即n=1；9点20分作为第二个计算人数的时间，即n=2；依此类推…，把一天内从上午9点到晚上24点分成了90个计算单位．
对第n个时刻进入园区的人数f（n）和时间n（n∈N^*）满足以下关系（如图1）：f（n）=

3600

(1≤n≤24)

3600•3

n-24

(25≤n≤36)

-300n+21600

(37≤n≤72)

(73≤n≤90)

，n∈N^*
对第n个时刻离开园区的人数g（n）和时间n（n∈N^*）满足以下关系（如图2）：g（n）=

0	(1≤n≤24)
500n-12000	(25≤n≤72)
5000	(73≤n≤90)

，n∈N^*
（1）试计算在当天下午3点整（即15点整）时，世博园区内共有多少游客？
（2）请求出当天世博园区内游客总人数最多的时刻．

查看答案和解析>>

科目：高中数学 来源： 题型：

某地区规划道路建设，考虑道路铺设方案，方案设计图中，求表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为（　　）

A．11

B．9

C．16

D．18

查看答案和解析>>

科目：高中数学 来源： 题型：

“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识，为此某网站进行了持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．

序号（i）	分组睡眠时间	组中值（m_i）	频数（人数）	频率（f_i）
1	[4，5）	4.5	8	0.04
2	[5，6）	5.5	52	0.26
3	[6，7）	6.5	60	0.30
4	[7，8）	7.5	56	0.28
5	[8，9）	8.5	20	0.10
6	[9，10]	9.5	4	0.02