练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2012•广东）如图所示，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．
    （1）证明：BD⊥平面PAC；
    （2）若PA=1，AD=2，求二面角B﹣PC﹣A的正切值．

    （1）见解析      （2）3

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    三棱锥及其侧视图、俯视图如图所示.设，分别为线段，的中点，为线段上的点，且.

    （1）证明：为线段的中点；
    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （13分）（2011•广东）如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，A，A′，B，B′分别为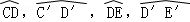的中点，O1，O1′，O2，O2′分别为CD，C′D′，DE，D′E′的中点．

    （1）证明：O1′，A′，O2，B四点共面；
    （2）设G为A A′中点，延长A′O1′到H′，使得O1′H′=A′O1′．证明：BO2′⊥平面H′B′G

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，ABCD是边长为2的正方形，,ED=1，//BD，且.
    （1）求证：BF//平面ACE；
    （2）求证：平面EAC平面BDEF;
    （3）求二面角B-AF-C的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，四棱锥中，⊥底面，底面为菱形，点为侧棱上一点.
    （1）若，求证：平面； 
    （2）若，求证：平面⊥平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，在四棱锥P-ABCD中，平面ABCD，AD//BC，BC=2AD，AC，Q是线段PB的中点.

    （1）求证：平面PAC；
    （2）求证：AQ//平面PCD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (2013·辽宁高考)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.

    (1)求证：平面PAC⊥平面PBC.
    (2)设Q为PA的中点,G为△AOC的重心,求证：QG∥平面PBC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，在四棱锥中，，，为正三角形，且平面平面．

    （1）证明：；
    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，四棱锥的底面为一直角梯形，侧面PAD是等边三角形，其中，,平面底面，是的中点．
     
    (1)求证：//平面；
    (2)求证：；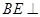
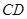    (3)求与平面所成角的正弦值。

    查看答案和解析>>

    同步练习册答案