
分析 根据三角函数$f(x)=3sin(2x+\frac{π}{3})$的图象与性质,对题目中的命题进行分析、判断,即可得出正确的命题序号.
解答 解:函数$f(x)=3sin(2x+\frac{π}{3})$,
对于①,f($\frac{11π}{2}$)=3sin(2×$\frac{11π}{2}$+$\frac{π}{3}$)=-$\frac{3\sqrt{3}}{2}$不是最值,
∴f(x)的图象C不关于直线x=$\frac{11π}{2}$对称,①错误;
对于②,f($\frac{π}{3}$)=3sin(2×$\frac{π}{3}$+$\frac{π}{3}$)=0,
∴f(x)的图象C关于点$(\frac{π}{3},0)$对称,②正确;
对于③,由y=3sin2x的图象向左平移$\frac{π}{3}$个单位长度,
得到y=3sin[2(x+$\frac{π}{3}$)]=3sin(2x+$\frac{2π}{3}$)的图象,不是图象C,③错误;
对于④,x∈(-$\frac{π}{12}$,$\frac{5π}{12}$)时,2x+$\frac{π}{3}$∈($\frac{π}{6}$,$\frac{7π}{6}$),
∴函数f(x)=3sin(2x+$\frac{π}{3}$)在区间(-$\frac{π}{12},\frac{5π}{12}$)内不是增函数,④错误;
对于⑤,|f(x+π)+1|=|3sin(2x+2π+$\frac{π}{3}$)+1|=|3sin(2x+$\frac{π}{3}$)+1|=|f(x)+1|,
∴|f(x)+1|的最小正周期为π,⑤正确.
综上,正确的结论序号是②⑤.
故答案为:②⑤.
点评 本题考查了三角函数的图象和性质及其变换的应用问题,是综合性题目.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
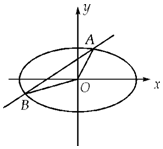 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com