
设 (
( 是正整数),利用赋值法解决下列问题:
是正整数),利用赋值法解决下列问题:
(1)求 ;
;
(2) 为偶数时,求
为偶数时,求 ;
;
(3) 是3的倍数时,求
是3的倍数时,求 。
。
科目:高中数学 来源: 题型:解答题
五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 展开式的二项式系数之和为256.
展开式的二项式系数之和为256.
(1)求 ;
;
(2)若展开式中常数项为 ,求
,求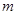 的值;
的值;
(3)若 展开式中系数最大项只有第6项和第7项,求
展开式中系数最大项只有第6项和第7项,求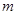 的取值情况.
的取值情况.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若四位数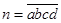 的各位数码
的各位数码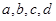 中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义
中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义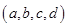 为的数码组,其中
为的数码组,其中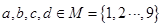 若 数码组为
若 数码组为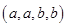 型,
型,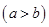 , 试求所有四位三角形数的个数.
, 试求所有四位三角形数的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com