
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)求出原函数的导函数,对![]() 分类求解原函数的单调区间;
分类求解原函数的单调区间;
(2)把证当![]() 时,
时,![]() ,转化为证
,转化为证![]() ,即证
,即证![]() .构造函数
.构造函数![]() ,
,![]() ,
,![]() ,利用导数分别求得
,利用导数分别求得![]() 和
和![]() ,则结论得证.
,则结论得证.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,解
时,解![]() ,得
,得![]() ,解
,解![]() ,得
,得![]() .
.
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;
上单调递减;
当![]() 时,解
时,解![]() ,得
,得![]() ,解
,解![]() ,得
,得![]() .
.
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;
上单调递减;
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;
上单调递减;
(2)证明:当![]() 时,
时,![]() ,
,
![]() 要证当
要证当![]() 时,
时,![]() ,只要证
,只要证![]() .
.
只要证![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
![]() 当
当![]() 时,
时,![]() (1)
(1)![]() ,当且仅当
,当且仅当![]() 时“
时“![]() ”成立;
”成立;
令![]() ,
,![]() ,则
,则![]() ,
,
解![]() ,得
,得![]() ,解
,解![]() ,得
,得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() .
.
![]() .
.
即当![]() 时,
时,![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】在线段![]() 的两端点各置一个光源,已知光源
的两端点各置一个光源,已知光源![]() ,
,![]() 的发光强度之比为
的发光强度之比为![]() ,则线段上光照度最小的一点到
,则线段上光照度最小的一点到![]() ,
,![]() 的距离之比为______(光学定律:
的距离之比为______(光学定律:![]() 点的光照度与
点的光照度与![]() 到光源的距离的平方成反比,与光源的发光强度成正比)
到光源的距离的平方成反比,与光源的发光强度成正比)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为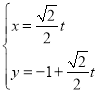 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的必要不充分条件;③命题“
”的必要不充分条件;③命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;④命题“若
”;④命题“若![]() ,则
,则![]() ”的逆命题为真命题.其中所有正确命题的序号是_________.
”的逆命题为真命题.其中所有正确命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线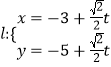 (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于点
相交于点![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程为(x-1)2+(y-1)2=9,P(2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com