
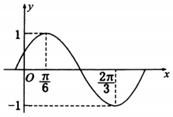
 函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示.分析 (Ⅰ)根据f(x)的部分图象求出A、ω以及φ的值即可;
(Ⅱ)求出f(x-$\frac{π}{12}$)=sin2x,化简函数F(x),
根据题意设t=sin2x,则由x∈[0,$\frac{π}{2}$]时t∈[0,1],
把F(x)=0化为3t2+mt+2=0在[0,1]上有两个不等的实数根,
由此求出实数m的取值范围.
解答 解:(Ⅰ)根据f(x)=Asin(ωx+φ)的部分图象知,
A=1,$\frac{T}{2}$=$\frac{2π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,
∴T=π,
∴ω=$\frac{2π}{T}$=2;
由“五点法画图”知,
2×$\frac{π}{6}$+φ=$\frac{π}{2}$,解得φ=$\frac{π}{6}$;
∴函数f(x)=sin(2x+$\frac{π}{6}$);
(Ⅱ)∵f(x-$\frac{π}{12}$)=sin(2x-$\frac{π}{6}$+$\frac{π}{6}$)=sin2x,
∴函数F(x)=3[f(x-$\frac{π}{12}$)]2+mf(x-$\frac{π}{12}$)+2
=3sin2(2x)+msin2x+2;
在区间[0,$\frac{π}{2}$]上有四个不同零点,
设t=sin2x,由x∈[0,$\frac{π}{2}$],得2x∈[0,π],即sin2x∈[0,1],
∴t∈[0,1],
令F(x)=0,则3t2+mt+2=0在[0,1]上有两个不等的实数根,
令g(t)=3t2+mt+2
则由$\left\{\begin{array}{l}{△>0}\\{g(0)≥0}\\{g(1)>0}\\{0<-\frac{m}{6}<1}\end{array}\right.$,解得-5<m<-2$\sqrt{6}$;
∴实数m的取值范围是-5<m<-2$\sqrt{6}$.
点评 本题考查了由部分图象求三角函数解析式的应用问题,也考查了函数零点与方程根的应用问题,是综合性问题.


科目:高中数学 来源: 题型:选择题
| A. | f(-2)<f(1)<f(3) | B. | f(1)<f(-2)<f(3) | C. | f(3)<f(-2)<f(1) | D. | f(-2)<f(3)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{a}{4}$)或(0,-$\frac{a}{4}$) | B. | (0,$\frac{1}{4a}$)或(0,-$\frac{1}{4a}$) | C. | $(0,\frac{1}{4a})$ | D. | $(\frac{1}{4a},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
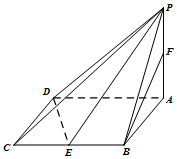 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,BC的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,BC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com