
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
【答案】C
【解析】解:∵函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),
+lnx),
∴函数f(x)的定义域是(0,+∞)
∴f′(x)= ![]() ﹣k(﹣
﹣k(﹣ ![]() +
+ ![]() )=
)= ![]()
∵x=2是函数f(x)的唯一一个极值点
∴x=2是导函数f′(x)=0的唯一根.
∴ex﹣kx=0在(0,+∞)无变号零点,
令g(x)=ex﹣kx
g′(x)=ex﹣k①k≤0时,g′(x)>0恒成立.g(x)在(0,+∞)时单调递增的
g(x)的最小值为g(0)=1,g(x)=0无解②k>0时,g′(x)=0有解为:x=lnk
0<x<lnk时,g′(x)<0,g(x)单调递减
lnk<x时,g′(x)>0,g(x)单调递增
∴g(x)的最小值为g(lnk)=k﹣klnk
∴k﹣klnk>0
∴k<e,
由y=ex和y=ex图象,它们切于(1,e),
综上所述,k≤e.
故选C
由f(x)的导函数形式可以看出,需要对k进行分类讨论来确定导函数为0时的根.


科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2+x>0},集合B= ![]() ,则(UA)∪B=( )
,则(UA)∪B=( )
A.[0,2)
B.[﹣1,0]
C.[﹣1,2)
D.(﹣∞,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.

本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() )x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
)x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
A.![]() b2﹣
b2﹣ ![]() b3
b3
B.![]() b﹣
b﹣ ![]()
C.0
D.2b﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
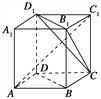
A. BD∥平面CB1D1 B. AC1⊥BD
C. AC1⊥平面CB1D1 D. 异面直线AD与CB1所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
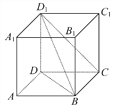
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com