
分析 (Ⅰ)利用综合法以及基本不等式直接证明 $\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}+abc≥2\sqrt{3}$;
(Ⅱ)通过a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,结合基本不等式证明 ${a^2}+{b^2}+{c^2}+{(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})^2}≥6\sqrt{3}$.
解答 证明:(Ⅰ)∵a,b,c为正实数∴$\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}≥3\root{3}{{\frac{1}{{{a^3}{b^3}{c^3}}}}}=\frac{3}{abc}$,当且仅当a=b=c时取等号.
∵$\frac{3}{abc}+abc≥2\sqrt{3}$,
∴$\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}+abc≥2\sqrt{3}$,当且仅当a=b=c时取等号…(5分)
(Ⅱ)∵a,b,c为正实数
∴a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac
∴a2+b2+c2≥ab+bc+ac,
同理 $\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}≥\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}$,${(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})^2}≥$$\frac{3}{ab}+\frac{3}{bc}+\frac{3}{ac}$
∴${a^2}+{b^2}+{c^2}+{(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})^2}≥$$ab+bc+ac+\frac{3}{ab}+\frac{3}{bc}+\frac{3}{ac}≥6\sqrt{3}$,
当且仅当a=b=c时取等号.…(10分)
点评 本题考查综合法以及基本不等式的应用,考查不等式的证明,考查逻辑推理能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
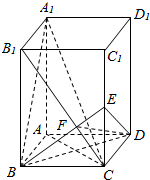 如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.
如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | ||
| C. | 4 | D. | 不确定,与k值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
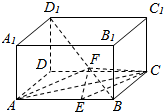 如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.
如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
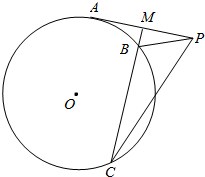 自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.
自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com