
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
分析 (1)作出女性用户和男性用户的频率分布表,由图可得女性用户更稳定.
(2)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,记为A,B,C,D,评分不小于90分的人数为2,记为a,b,设事件M为“两名用户评分都小于90分”从6人人任取2人,利用列举法能求出两名用户中评分都小于90分的概率.
解答 (本小题满分12分)
解:(1)女性用户和男性用户的频率分布表分别如下左、右图:
由图可得女性用户更稳定.(4分)
(2)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,
其中评分小于90分的人数为4,记为A,B,C,D,
评分不小于90分的人数为2,记为a,b,
设事件M为“两名用户评分都小于90分”从6人人任取2人,
基本事件空间为Ω={(AB),(AC),(AD),(Aa),(Ab),
(BC),(BD),(Ba),(Bb),(CD),(Ca),(Cb),
(Da),(Db),(ab)},共有15个元素.
M={(AB),(AC),(AD),(BC),(BD),(CD)},共有6个元素.
P(M)=$\frac{6}{15}=\frac{2}{5}$.(12分)
点评 本小题主要考查学生对概率统计知识的理解,以及统计案例的相关知识,同时考查学生的数据处理能力.


科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | $\frac{11}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
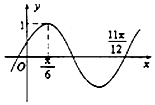 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
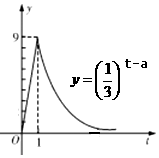 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com