
 和判断力
和判断力 进行统计分析,得下表数据:
进行统计分析,得下表数据: |  |  |  |  |
 |  |  |  |  |
 关于
关于 的线性回归方程
的线性回归方程 中的
中的 的值为
的值为 ,则记忆力为
,则记忆力为 的同学的判断力约为(附:线性回归方程
的同学的判断力约为(附:线性回归方程 中,
中, ,其中
,其中 、
、 为样本平均值)( )
为样本平均值)( ) B.
B. C.
C. D.
D.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源:不详 题型:填空题
| 1 |
| n |
| . |
| x |
| . |
| x |
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出 关于
关于 的线性回归方程:
的线性回归方程: ,那么表中
,那么表中 的值为( )
的值为( )
| A.3 | B.3.15 | C.4.5 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示转速(单位转/秒),用
表示转速(单位转/秒),用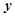 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).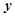 与
与 之间有线性相关关系,求
之间有线性相关关系,求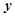 对
对 的回归直线方程.
的回归直线方程. )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 =bx+a.
=bx+a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com