
分析 由题可知2是x2+ax+b=0的根,求得b=-2a-4,代入消去零因子x-2,求得$\frac{4+a}{3}$=2,即可求得a和b的值.
解答 解:$\underset{lim}{x→2}$$\frac{{x}^{2}+ax+b}{{x}^{2}-x-2}$=$\underset{lim}{x→2}$$\frac{{x}^{2}+ax+b}{(x-2)(x+1)}$=2,
∴2是x2+ax+b=0的根,
∴2a+b+4=0,
b=-2a-4,
$\underset{lim}{x→2}$$\frac{{x}^{2}+ax+b}{{x}^{2}-x-2}$,
=$\underset{lim}{x→2}$$\frac{{x}^{2}+ax-2a-4}{(x-2)(x-1)}$,
=$\underset{lim}{x→2}$$\frac{(x-2)(x+2+a)}{(x-2)(x+1)}$,
=$\underset{lim}{x→2}$$\frac{x+2+a}{x+1}$,
∴$\frac{4+a}{3}$=2,
解得:a=2,b=-8,
常数a,b分别为2,-8.
点评 本题考查极限的性质和应用,解题时注意审题,仔细解答,注意合理的等价转化,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
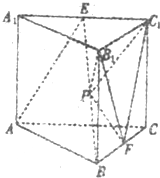 在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com