
【题目】将函数f(x)=3sin(﹣3x![]() )﹣2的图象向右平移
)﹣2的图象向右平移![]() 个单位长度得到函数g(x)的图象,若g(x)在区间[
个单位长度得到函数g(x)的图象,若g(x)在区间[![]() ,θ]上的最大值为1,则θ的最小值为( )
,θ]上的最大值为1,则θ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=log2(|x+1|+|x﹣2|﹣m).
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,
,![]() 是直线上
是直线上![]() 一点,过点
一点,过点![]() 做抛物线的两条切线,切点分别为
做抛物线的两条切线,切点分别为![]() ,
,![]() ,
,![]() 是抛物线上异于
是抛物线上异于![]() ,
,![]() 的任一点,抛物线在
的任一点,抛物线在![]() 处的切线与
处的切线与![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,则
,则![]() 外接圆面积的最小值为______.
外接圆面积的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试判断方程
时,试判断方程![]() 是否有实数解,并说明理由.
是否有实数解,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为自然对数的底数) .
为自然对数的底数) .
(1)若![]() 在
在![]() 处的取得极值为1,求
处的取得极值为1,求![]() 及
及![]() 的值;
的值;
(2)![]() 时,讨论函数
时,讨论函数![]() 的极值;
的极值;
(3)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个棱锥的底面是正方形,且顶点在底面内的射影是底面的中心,那么这样的棱锥叫正四棱锥.若一正四棱锥的体积为18,则该正四棱锥的侧面积最小时,以下结论正确的是( ).
A.棱的高与底边长的比为![]() B.侧棱与底面所成的角为
B.侧棱与底面所成的角为![]()
C.棱锥的高与底面边长的比为![]() D.侧棱与底面所成的角为
D.侧棱与底面所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: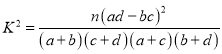
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com