
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+3.
(1)求{an}的通项公式;
(2)若数列{bn},满足anbn=log3an , 求{bn}的前n项和Tn .
【答案】
(1)解:因为2Sn=3n+3,所以2a1=31+3=6,故a1=3,
当n>1时,2Sn﹣1=3n﹣1+3,
此时,2an=2Sn﹣2Sn﹣1=3n﹣3n﹣1=2×3n﹣1,即an=3n﹣1,
所以an= ![]() .
.
(2)解:因为anbn=log3an,所以b1= ![]() ,
,
当n>1时,bn=31﹣nlog33n﹣1=(n﹣1)×31﹣n,
所以T1=b1= ![]() ;
;
当n>1时,Tn=b1+b2+…+bn= ![]() +(1×3﹣1+2×3﹣2+…+(n﹣1)×31﹣n),
+(1×3﹣1+2×3﹣2+…+(n﹣1)×31﹣n),
所以3Tn=1+(1×30+2×3﹣1+3×3﹣2+…+(n﹣1)×32﹣n),
两式相减得:2Tn= ![]() +(30+3﹣1+3﹣2+…+32﹣n﹣(n﹣1)×31﹣n)=
+(30+3﹣1+3﹣2+…+32﹣n﹣(n﹣1)×31﹣n)= ![]() +
+ ![]() ﹣(n﹣1)×31﹣n=
﹣(n﹣1)×31﹣n= ![]() ﹣
﹣ ![]() ,
,
所以Tn= ![]() ﹣
﹣ ![]() ,经检验,n=1时也适合,
,经检验,n=1时也适合,
综上可得Tn= ![]() ﹣
﹣ ![]()
【解析】(1)利用2Sn=3n+3,可求得a1=3;当n>1时,2Sn﹣1=3n﹣1+3,两式相减2an=2Sn﹣2Sn﹣1 , 可求得an=3n﹣1 , 从而可得{an}的通项公式;(2)依题意,anbn=log3an , 可得b1= ![]() ,当n>1时,bn=31﹣nlog33n﹣1=(n﹣1)×31﹣n , 于是可求得T1=b1=
,当n>1时,bn=31﹣nlog33n﹣1=(n﹣1)×31﹣n , 于是可求得T1=b1= ![]() ;当n>1时,Tn=b1+b2+…+bn=
;当n>1时,Tn=b1+b2+…+bn= ![]() +(1×3﹣1+2×3﹣2+…+(n﹣1)×31﹣n),利用错位相减法可求得{bn}的前n项和Tn .
+(1×3﹣1+2×3﹣2+…+(n﹣1)×31﹣n),利用错位相减法可求得{bn}的前n项和Tn .
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系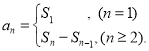 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一同学在电脑中打出如下若干个圆:○●○○●○○○●○○○○●○○○○○●…,若依此规律继续下去,得到一系列的圆,则在前2012个圆中共有●的个数是( )
A.61
B.62
C.63
D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4
,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4 ![]() .
. 
(1)求椭圆的方程;
(2)如图,直线x=ty+m交椭圆于不同两点C,D,若以线段CD为直径的圆过原点O,求|CD|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}分别满足a1=1,|an+1﹣an|=2,且 ![]() |=2,其中n∈N* , 设数列{an},{bn}的前n项和分别为Sn , Tn .
|=2,其中n∈N* , 设数列{an},{bn}的前n项和分别为Sn , Tn .
(1)若数列{an},{bn}都是递增数列,求数列{an},{bn}的通项公式;
(2)若数列{cn}满足:存在唯一的正整数k(k≥2),使得ck<ck﹣1 , 则称数列{cn}为“k坠点数列”. ①若数列{an}为“5坠点数列”,求Sn;
②若数列{an}为“p坠点数列”,数列{bn}为“q坠点数列”,是否存在正整数m使得Sm+1=Tm?若存在,求出m的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”. 
(1)求男生跳远成绩的中位数.
(2)根据男女生的不同,用分层抽样的方法从该班学生中抽取1个容量为5的样本,求抽取的5人中女生的人数.
(3)以此作为样本,估计该校五年级学生体质的合格率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点M(1, ![]() ),N(﹣4,﹣
),N(﹣4,﹣ ![]() ),给出下列曲线方程:
),给出下列曲线方程:
①4x+2y﹣1=0;
②x2+y2=3;
③ ![]() +y2=1;
+y2=1;
④ ![]() ﹣y2=1.
﹣y2=1.
在曲线上存在点P满足|MP|=|NP|的所有曲线方程是( )
A.①③
B.②④
C.①②③
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且a,b,c成等差数列,有下列四个结论:①b2≥ac;② ![]() ;③
;③ ![]() ;④
;④ ![]() .其中正确的结论序号为 .
.其中正确的结论序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com