【题目】下面有5个命题：
①函数
的最小正周期是
；
②终边在
轴上的角的集合是
；
③在同一坐标系中，函数
的图象和函数
的图象有3个公共点；
④把函数
的图象向右平移
得到
的图象；
⑤角
为第一象限角的充要条件是
．
其中，真命题的编号是______（写出所有真命题的编号）．
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】《中华人民共和国个人所得税法》规定，公民月收入总额（工资、薪金等）不超过免征额的部分不必纳税，超过免征额的部分为全月应纳税所得额，个人所得税税款按税率表分段累计计算.为了给公民合理减负，稳步提升公民的收入水平，自2018年10月1日起，个人所得税免征额和税率进行了调整，调整前后的个人所得税税率表如下：
（1）已知小李2018年9月份上交的税费是295元，10月份月工资、薪金等税前收入与9月份相同，请帮小李计算一下税率调整后小李10月份的税后实际收入是多少？
（2）某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入，并制成下面的频率分布直方图.
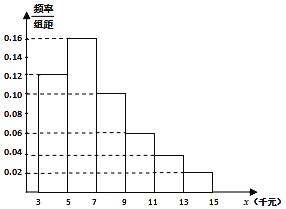
（ⅰ）请根据频率分布直方图估计该公司员工税前收入的中位数；
（ⅱ）同一组中的数据以这组数据所在区间中点的值作代表，按调整后税率表，试估计小李所在的公司员工该月平均纳税多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于数列
，称
（其中
）为数列的前k项“波动均值”.若对任意的，都有
，则称数列为“趋稳数列”．
（1）若数列1，
，2为“趋稳数列”，求的取值范围；
（2）若各项均为正数的等比数列
的公比
，求证：是“趋稳数列”；
（3）已知数列的首项为1，各项均为整数，前
项的和为
. 且对任意，都有
， 试计算：
（
）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列
满足
，其中A，B是两个确定的实数，
（1）若
，求的前n项和；
（2）证明：不是等比数列；
（3）若
，数列中除去开始的两项外，是否还有相等的两项，并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，
满足
，且
．正项数列
满足
，其前7项和为42．
（1）求数列和的通项公式；
（2）令
，数列
的前项和为
，若对任意正整数，都有
，求实数
的取值范围；
（3）将数列，的项按照“当为奇数时，
放在前面；当为偶数时，
放在前面”的要求进行排列，得到一个新的数列：
，
，
，
，
，
，
，
，
，
，
，…，求这个新数列的前项和
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,在平行四边形ABCD中,
,四边形ACEF为正方形,且平面
平面ACEF.
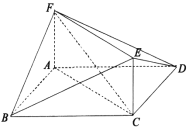
(1)证明:
;
(2)求平面BEF与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知
为等边三角形，
为等腰直角三角形，
.平面
平面ABD，点E与点D在平面ABC的同侧，且
，
.点F为AD中点，连接EF.
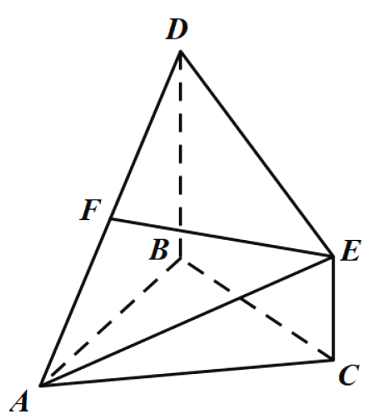
（1）求证：
平面ABC；
（2）求证：平面
平面ABD.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国家大力提倡科技创新，某工厂为提升甲产品的市场竞争力，对生产技术进行创新改造，使甲产品的生产节能降耗．以下表格提供了节能降耗后甲产品的生产产量
(吨)与相应的生产能耗
(吨)的几组对照数据．
|
|
|
|
|
|
|
|
|
|
（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（
，
）
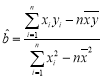（2）已知该厂技术改造前生产
吨甲产品的生产能耗为
吨，试根据（1）求出的线性回归方程，预测节能降耗后生产吨甲产品的生产能耗比技术改造前降低多少吨？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
