
解:∵f(-1)=a-b,-1≤f(-1)≤2,∴-1≤a-b≤2.
∵f(1)=a+b,2≤f(1)≤4,∴2≤a+b≤4.
∴a、b满足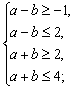
f(-2)=

作直线l:
把直线平移至l1的位置时,直线经过可行域上的点B,且与原点的距离最大;把直线l平移至l2的位置时,直线经过可行域上的点D,且与原点的距离最小.
由![]() 得B点的坐标为(3,1);
得B点的坐标为(3,1);
由![]() 得D点的坐标为(
得D点的坐标为(![]() ,
,![]() ).
).
∴f(-2)的最大值为f(-2)=
f(-2)的最小值为f(-2)=4×![]() -2×
-2×![]() =-1.
=-1.
∴-1≤f(-2)≤10为所求.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
| ax2+bx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com