
| A. | ($\frac{1}{n}$,$\frac{1}{m}$) | B. | ($\frac{1}{m}$,$\frac{1}{n}$) | C. | (-∞,$\frac{1}{n}$)∪($\frac{1}{m}$,+∞) | D. | (-∞,$\frac{1}{m}$)∪($\frac{1}{n}$,+∞) |
分析 依题意,a<0,m+n=-$\frac{b}{a}$,mn=$\frac{c}{a}$>0,从而可求得b,c,代入cx2+bx+a<0即可求得答案.
解答 解:∵不等式ax2+bx+c>0的解集为(m,n)(0<m<n),
∴a<0,m+n=-$\frac{b}{a}$,mn=$\frac{c}{a}$,
∴b=-a(m+n),c=amn,
∴cx2+bx+a<0?amnx2-a(m+n)x+a<0,
∵a<0,
∴mnx2-(m+n)x+1>0,
即(mx-1)(nx-1)>0,又0<m<n,
∴$\frac{1}{m}$>$\frac{1}{n}$,
∴x>$\frac{1}{m}$或x<$\frac{1}{n}$,
故不等式cx2+bx+a<0的解集是(-∞,$\frac{1}{n}$)∪($\frac{1}{m}$,+∞).
故选:C.
点评 本题考查,一元二次不等式的解法,求得b=-a(m+n),c=amn(a<0),是关键,考查转化与运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2-\frac{{2\sqrt{3}}}{3},2+\frac{{2\sqrt{3}}}{3}]$ | B. | $[1,2+\frac{{2\sqrt{3}}}{3}]$ | C. | $[2-\frac{{2\sqrt{3}}}{3},3]$ | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
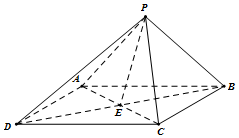 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com