
【题目】设函数![]() ,若方程
,若方程![]() 恰有两个不相等的实根
恰有两个不相等的实根![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】令g(x)=f(f(x))=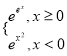 ,
,
∵y=f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,
∴g(x)=f(f(x))在(﹣∞,0)上单调递减,在(0,+∞)上单调递增.
做出g(x)=f(f(x))的函数图象如图所示:
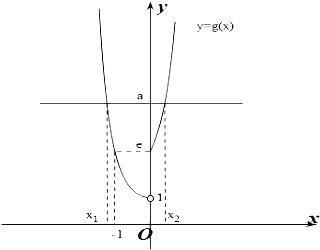
∵方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,
不妨设x1<x2,则x1≤﹣1,x2≥0,且f(x1)=f(x2),即x12=![]() .
.
∴![]() ,
,
令h(x1)=![]() ,则h′(x1)=
,则h′(x1)=![]() ,
,
∴当x1<﹣2时,h′(x1)>0,当﹣2<x1<﹣1时,h′(x1)<0,
∴h(x1)在(﹣∞,﹣2)上单调递增,在(﹣2,﹣1)上单调递减,
∴当x1=﹣2时,h(x1)取得最大值h(﹣2)=![]() .
.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时, ![]() 平均增加
平均增加![]() 个单位;
个单位;
③老师在某班学号为1~50的50名学生中依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样;
其中正确的个数是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 0
D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.
(1)求轨迹E的方程;
(2)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|a﹣1≤x≤2a+3},B={x|﹣2≤x≤4},全集U=R
(1)当a=2时,求A∪B和(RA)∩B;
(2)若A∩B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a值;
(2)判断并证明该函数在定义域R上的单调性;
(3)设关于x的函数F(x)=f(4x﹣b)+f(﹣2x+1)有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x)其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com