
【题目】某粮食店经销小麦,年销售量为6000千克,每千克小麦进货价为2.8元,销售价为3.4元,全年进货若干次,每次的进货量均为![]() 千克(
千克(![]() ),运费为100元/次,并且全年小麦的总存储费用为
),运费为100元/次,并且全年小麦的总存储费用为![]() 元.
元.
(1)用![]() (千克)表示该粮食店经销小麦的年利润
(千克)表示该粮食店经销小麦的年利润![]() (元);
(元);
(2)每次进货量为多少千克时,能使年利润![]() 最大?
最大?
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A'B'C'D'棱长为2,并且E,F分别是棱AA',CC'的中点.

(Ⅰ)求证:平面BED'F⊥平面BB'D'D;
(Ⅱ)求直线A'B'与平面BED'F所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
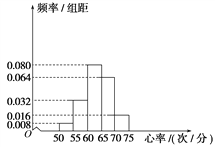
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含![]() 的频率。
的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
|
|
|
|
|
|
|
|
|
|
|
|
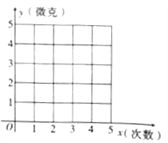
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]()
![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为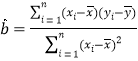 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com