
分析 根据对数的运算性质计算即可.
解答 解:log63•log612+(log62)2-27${\;}^{\frac{2}{3}-lo{g}_{3}2}$
=log63•(${log}_{6}^{3}$+${log}_{6}^{4}$)+(log62)2-9-${log}_{3}^{2}$
=${{(log}_{6}^{3})}^{2}$+2${log}_{6}^{3}$${log}_{6}^{2}$+${{(log}_{6}^{2})}^{2}$-9-${log}_{3}^{2}$
=${{(log}_{6}^{3}{+log}_{6}^{2})}^{2}$-9-${log}_{3}^{2}$
=-8-${log}_{3}^{2}$,
故答案为:-8-${log}_{3}^{2}$.
点评 本题考察了对数的运算,熟练掌握运算性质是解题的关键,本题是一道基础题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 5 | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-1,1) | B. | (3,1,-1) | C. | (3,-1,-1) | D. | (3,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
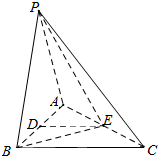 如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.
如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com