
分析 根据已知中函数$f(x)=\frac{{{x^2}+3}}{{{x^2}-4}}$的解析式,画出函数的图象,数形结合,可得函数的定义域,奇偶性,单调性等性质.
解答 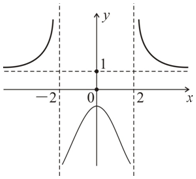 (本小题满分12分)
(本小题满分12分)
解:(1)函数的定义域为{x/x∈R,x≠±2}…(1分)
(2)函数的奇偶性:∵$f(-x)=\frac{{{{({-x})}^2}+3}}{{{{({-x})}^2}-4}}=\frac{{{x^2}+3}}{{{x^2}-4}}=f(x)$
∴f(x)是偶函数…(3分)
(3)∵$f(x)=\frac{{{x^2}+3}}{{{x^2}-4}}=1+\frac{7}{{{x^2}-4}}≠1$,当x∈[0,2)时,$f(x)≤-\frac{3}{4}$且递减;
当x∈(2,+∞)时,f(x)>1,递减且以直线x=2,y=1为渐近线;
又f(x)是偶函数
∴f(x)当x∈(-2,0]时,$f(x)≤-\frac{3}{4}$且递增;
当x∈(-∞,-2)时,f(x)>1,递增且以直线x=-2,y=1为渐近线;…(8分)
(4)函数f(x)的图象如图所示.…(12分)
点评 本题考查的知识点是函数的图象,函数的性质,本题中的函数即为所谓的“囧函数”,要求学生掌握.


科目:高中数学 来源: 题型:选择题
| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{-\frac{1}{2}}}$ | B. | y=x-2 | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-\frac{3}{2})<f(-1)<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-1)<f(-\frac{3}{2})<f(2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com