
【题目】下列结论正确的是( )
A.存在每个面都是直角三角形的四面体
B.每个面都是三角形的几何体是三棱锥
C.圆台上、下底面圆周上各取一点的连线是母线
D.用一个平面截圆锥,截面与底面间的部分是圆台
【答案】A
【解析】
利用椎体、台体的结构特征即可逐一判断.
对于A,利用三棱锥![]() ,满足
,满足![]() 平面
平面![]() ,
,
且![]() 是以点
是以点![]() 为直角顶点的直角三角形, 如图:
为直角顶点的直角三角形, 如图:

则![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,故三棱锥
,故三棱锥![]() 的四个面都是直角三角形,
的四个面都是直角三角形,
![]() 存在每个面都是直角三角形的四面体.
存在每个面都是直角三角形的四面体.
对于B,根据三棱锥的结构特征,各个面为三角形不一定为三棱锥,
两个一样的三棱锥上下拼接成一个六面体,它的每个面都是三角形,故B错误;
对于C,以直角梯形垂直于底边的腰所在的直线为旋转轴,
其余各边旋转而形成的曲面所围成的几何体叫做圆台,
旋转轴叫做圆台的轴,直角梯形上、下底旋转所成的圆面称为圆台的上、下底面,
另一腰旋转所成的曲面称为圆台的侧面,
侧面上各个位置的直角梯形的腰称为圆台的母线,故C错误;
对于D,只有用平行于圆锥底面的平面去截取圆锥,
圆锥底面和截面之间的部分才是圆台,故D错误;
故选:A


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 22 | ▲ | 30 |
女 | ▲ | 12 | ▲ |
总计 | ▲ | ▲ | 50 |
表1
并邀请这30名男生参加盲拧三阶魔方比赛,其完成情况如下表所示:
成功完成时间(分钟) |
|
|
|
|
人数 | 10 | 10 | 5 | 5 |
表2
(1)将表1补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(2)根据表2中的数据,求这30名男生成功完成盲拧的平均时间(同一组中的数据用该组区间的中点值代替);附参考公式及数据: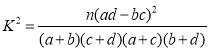 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
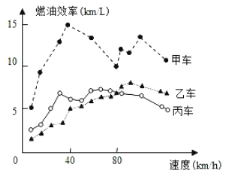
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了了解高中新生的体能情况,某学校抽取部分高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从 左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12﹒
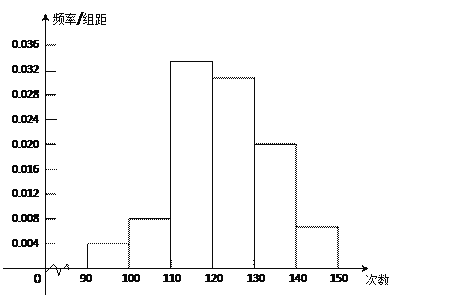
[来
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(Ⅲ)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A.每人都安排一项工作的不同方法数为54
B.每人都安排一项工作,每项工作至少有一人参加,则不同的方法数为![]()
C.如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为![]()
D.每人都安排一项工作,每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com