
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
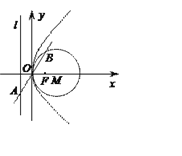
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
【答案】(1)(x-2)2+y2=4。 (2)2.(3)![]() .
.
【解析】试题分析:(1)根据![]() 可求出
可求出![]() 的值,从而求出抛物线方程,求出圆心和半径可求出
的值,从而求出抛物线方程,求出圆心和半径可求出![]() 的方程;(2)先表示出
的方程;(2)先表示出![]() 然后根据点在抛物线上将
然后根据点在抛物线上将![]() 消去,求关于
消去,求关于![]() 的二次函数的最小值即可;(3)以点
的二次函数的最小值即可;(3)以点![]() 这圆心,
这圆心,![]() 为半径作
为半径作![]() ,则线段
,则线段![]() 即为
即为![]() 与
与![]() 的公共弦,设点
的公共弦,设点![]() ,根据
,根据![]() ,求出直线
,求出直线![]() 的方程,使直线与
的方程,使直线与![]() 无关,可求出定点坐标.
无关,可求出定点坐标.
试题解析:(1)因为=OA·cos60°=2×=1,即p=2,所以抛物线C的方程为y2=4x
设⊙M的半径为r,则r=![]() ·
·![]() =2,所以⊙M的方程为(x-2)2+y2=4。
=2,所以⊙M的方程为(x-2)2+y2=4。
(2)设P(x,y)(x≥0),则![]() ·
·![]() =(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
=(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
所以当x=0时,![]() ·
·![]() 有最小值为2.
有最小值为2.
(3)以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦.
设点Q(-1,t),则QS2=QM2-4=t2+5,所以⊙Q的方程为(x+1)2+(y-t)2=t2+5,
从而直线QS的方程为3x-ty-2=0(*),
因为![]() 一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).
一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,曲线BCD为抛物线的一部分.
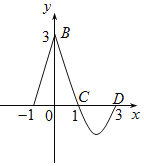
(Ⅰ)求f(x)解析式;
(Ⅱ)若f(x)=1,求x的值;
(Ⅲ)若f(x)>f(2-x),求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3-![]() x2+1(xR),其中a>0.
x2+1(xR),其中a>0.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是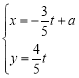 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 为直线
为直线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(2)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
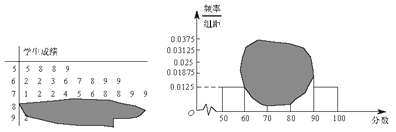
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
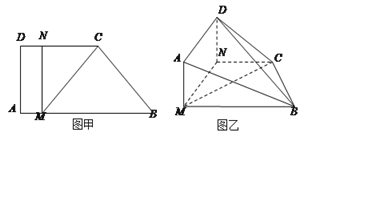
【题目】如图甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 与平面
与平面![]() 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(II)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com