
【题目】广州亚运会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向广州亚组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元.(
元.(![]() )
)
(1)写出该专营店一年内销售这种纪念章所获利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出最大值.
(元)最大,并求出最大值.
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】随着人们经济收入的不断增加,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)求线性回归方程![]() ;
;
(2)估计使用年限为12年时,使用该款车的总费用是多少万元?
线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下: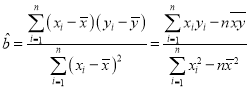 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 表示三条不同的直线,
表示三条不同的直线,![]() ,
,![]() ,
,![]() 表示三个不同的平面,给出下列四个结论:
表示三个不同的平面,给出下列四个结论:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() 是
是![]() 在
在![]() 内的射影,
内的射影,![]() ,则
,则![]() ;
;
③若![]() 是平面
是平面![]() 的一条斜线,
的一条斜线,![]() ,
,![]() 为过
为过![]() 的一条动直线,则可能有
的一条动直线,则可能有![]() 且
且![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的个数为( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
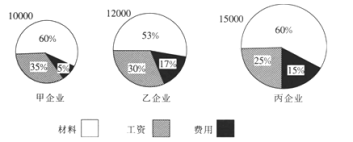
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区![]() 名居民参加
名居民参加![]() 年国庆活动,他们的年龄在
年国庆活动,他们的年龄在![]() 岁至
岁至![]() 岁之间,将年龄按
岁之间,将年龄按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到的频率分布直方图如图所示.
分组,得到的频率分布直方图如图所示.
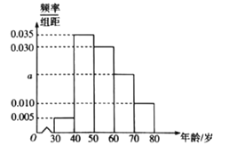
(1)求![]() 的值,并求该社区参加
的值,并求该社区参加![]() 年国庆活动的居民的平均年龄(每个分组取中间值作代表);
年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在![]() 、
、![]() 的人员中按分层抽样的方法抽取
的人员中按分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行座谈,用
人进行座谈,用![]() 表示参与座谈的居民的年龄在
表示参与座谈的居民的年龄在![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地![]() 岁至
岁至![]() 岁之间的市民中抽取
岁之间的市民中抽取![]() 名进行调查,其中有
名进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() ,当
,当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com