
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为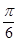 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明过程详见解析;(2)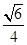 .
.
解析试题分析:(1)可以遵循思路面面垂直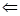 线面垂直
线面垂直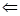 线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明
线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明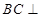 面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即
面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即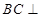 BD,
BD, 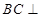 PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
(2)求线面夹角可以利用三维空间直角坐标系,分别以DA,DB,PD三条两两垂直的直线建立坐标系,求面法向量与直线的夹角的余弦值的绝对值即为线面夹角的余弦值.
试题解析:
(1)∵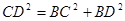 ∴
∴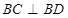
又∵ ⊥底面
⊥底面 ∴
∴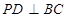
又∵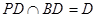 ∴
∴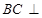 平面
平面
而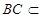 平面
平面 ∴平面
∴平面 平面
平面 5分
5分
(1)由(1)所证,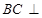 平面
平面 ,所以∠
,所以∠ 即为二面角P-BC-D的平面角,即∠
即为二面角P-BC-D的平面角,即∠
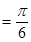
而 ,所以
,所以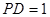 7分
7分
分别以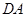 、
、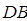 、
、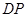 为
为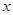 轴、
轴、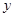 轴、
轴、 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则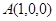 ,
,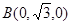 ,
,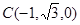 ,
, 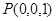 ,所以,
,所以,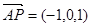 ,
,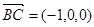 ,
,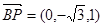 ,设平面
,设平面 的法向量为
的法向量为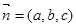 ,则
,则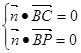 ,即
,即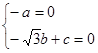 可解得
可解得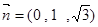 ∴
∴ 与平面
与平面 所成角的正弦值为
所成角的正弦值为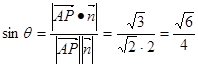 12分
12分
考点:面面垂直 线面夹角


科目:高中数学 来源: 题型:解答题
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=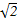 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.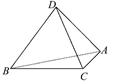
(1)当平面ADB⊥平面ABC时,求CD.
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.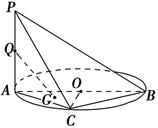
(1)求证:BC⊥平面PAC;
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥S—ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°。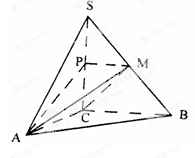
(1)求证:平面MAP⊥平面SAC。
(2)求二面角M—AC—B的平面角的正切值;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且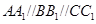 ,
,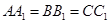 .
.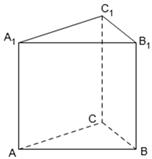
(1)求证:平面 //平面
//平面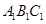 ;
;
(2)若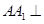 平面
平面 ,且
,且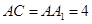 ,
,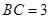 ,
,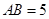 ,求证:
,求证: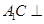 平面
平面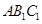 ;
;
(3)在(2)的条件下,求二面角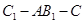 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com