
【题目】已知下列两个命题,命题甲:平面α与平面β相交;命题乙:相交直线l,m都在平面α内,并且都不在平面β内,直线l,m中至少有一条与平面β相交.则甲是乙的( )
A.充分且必要条件B.充分而不必要条件
C.必要而不充分条件D.既不充分也不必要条件
【答案】A
【解析】
由题意此问题等价于判断:①命题:已知相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,且都不在平面
内,且都不在平面![]() 内,若
内,若![]() ,
,![]() 中至少有一条与
中至少有一条与![]() 相交,则平面
相交,则平面![]() 与平面
与平面![]() 相交;②命题:已知相交直线
相交;②命题:已知相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内,若
内,若![]() 与
与![]() 相交,则
相交,则![]() ,
,![]() 中至少有一条与
中至少有一条与![]() 相交这两个命题的真假;分别判断分析可得答案.
相交这两个命题的真假;分别判断分析可得答案.
解:由题意此问题等价于判断
①命题:已知相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,且都不在平面
内,且都不在平面![]() 内,若
内,若![]() ,
,![]() 中至少有一条与
中至少有一条与![]() 相交,则平面
相交,则平面![]() 与平面
与平面![]() 相交,
相交,
②命题:已知相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内,若
内,若![]() 与
与![]() 相交,则
相交,则![]() ,
,![]() 中至少有一条与
中至少有一条与![]() 相交的真假;
相交的真假;
对于①命题此处在证明必要性,因为平面![]() 内两相交直线
内两相交直线![]() 和
和![]() 至少一个与
至少一个与![]() 相交,不妨假设直线
相交,不妨假设直线![]() 与
与![]() 相交,交点为
相交,交点为![]() ,则
,则![]() 属于
属于![]() 同时属于
同时属于![]() 面,所以
面,所以![]() 与
与![]() 有公共点,且由相交直线
有公共点,且由相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 可知平面
可知平面![]() 与
与![]() 必相交故①命题为真
必相交故①命题为真
对于②命题此处在证充分性,因为平![]() 与
与![]() 相交,且两相交直线
相交,且两相交直线![]() 和
和![]() 都在平面
都在平面![]() 内,且都不在平面
内,且都不在平面![]() 内,若
内,若![]() ,
,![]() 都不与
都不与![]() 相交,则
相交,则![]() ,
,![]() 平行平面
平行平面![]() ,那么
,那么![]() ,这与
,这与![]() 相交矛盾,故②命题也为真.
相交矛盾,故②命题也为真.
故选:A.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】动点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,已知点
,已知点![]() 的轨迹是过点
的轨迹是过点![]() 的圆.
的圆.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 在
在![]() 轴的同侧),
轴的同侧),![]() ,
,![]() 为椭圆的左、右焦点,若
为椭圆的左、右焦点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周礼夏官马质》中记载“马量三物:一日戎马,二日田马,三日驽马”,其意思为马按照品种可以分为三个等级,一等马为戎马,二等马为田马,三等马为驽马.假设在唐朝的某个王爷要将7匹马(戎马3匹,田马、驽马各2匹)赏赐给甲、乙、丙3人,每人至少2匹,则甲和乙都得到一等马的分法总数为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周.则“课程‘乐’不排在第一周,课程‘御’不排在最后一周”的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() ,平面
,平面![]() 平面
平面![]() .
.
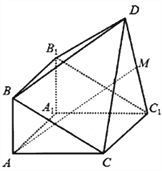
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为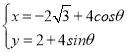 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为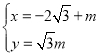 (m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(1)求曲线C的极坐标方程;
(2)直线l与曲线C相交于M,N两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,从P中任取2个元素,分别记为a,b.
,从P中任取2个元素,分别记为a,b.
(1)若![]() ,随机变量X表示ab被3除的余数,求
,随机变量X表示ab被3除的余数,求![]()
![]() 的概率;
的概率;
(2)若![]() (
(![]() 且
且![]() ),随机变量Y表示
),随机变量Y表示![]() 被5除的余数,求Y的概率分布及数学期望
被5除的余数,求Y的概率分布及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为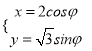 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎是一种急性感染性肺炎,其病原体是一种先前未在人类中发现的新型冠状病毒,即2019新型冠状病毒.2020年2月7日,国家卫健委决定将“新型冠状病毒感染的肺炎”暂命名为“新型冠状病毒肺炎”,简称“新冠肺炎”.患者初始症状多为发热、乏力和干咳,并逐渐出现呼吸困难等严重表现.基于目前流行病学调查,潜伏期为1~14天,潜伏期具有传染性,无症状感染者也可能成为传染源.某市为了增强民众防控病毒的意识,举行了“预防新冠病毒知识竞赛”网上答题,随机抽取![]() 人,答题成绩统计如图所示.
人,答题成绩统计如图所示.
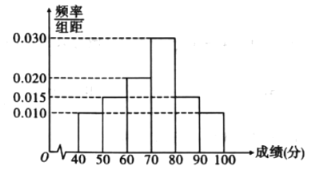
(1)由直方图可认为答题者的成绩![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 分别为答题者的平均成绩
分别为答题者的平均成绩![]() 和成绩的方差
和成绩的方差![]() ,那么这
,那么这![]() 名答题者成绩超过
名答题者成绩超过![]() 分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
(2)如果成绩超过![]() 分的民众我们认为是“防御知识合格者”,用这
分的民众我们认为是“防御知识合格者”,用这![]() 名答题者的成绩来估计全市的民众,现从全市中随机抽取
名答题者的成绩来估计全市的民众,现从全市中随机抽取![]() 人,“防御知识合格者”的人数为
人,“防御知识合格者”的人数为![]() ,求
,求![]() .(精确到
.(精确到![]() )
)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com