
【题目】已知函数f(x)=ax(lnx﹣1)﹣x2(a∈R)恰有两个极值点x1 , x2 , 且x1<x2 . (Ⅰ)求实数a的取值范围;
(Ⅱ)若不等式lnx1+λlnx2>1+λ恒成立,求实数λ的取值范围.
【答案】解:(Ⅰ)∵f(x)=ax(lnx﹣1)﹣x2(a∈R), ∴f′(x)=alnx﹣2x,
依题意得x1 , x2是alnx﹣2x=0的两个不等正实数根,
∴a≠0, ![]() ,
,
令g(x)= ![]() ,
, ![]() ,
,
当x∈(0,e)时,g′(x)>0;当x∈(e,+∞)时,g′(x)<0,
∴g(x)在(0,e)上单调递增,在(e,+∞)上单调递减,且g(1)=0,
当x>e时,g(x)>0,
∴0< ![]() <g(e)=
<g(e)= ![]() ,
,
解得a>2e,故实数a的取值范围是(2e,+∞).
(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 ,
两式相减,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2 ![]() ,
,
∴lnx1+λlnx2>1+λ,∴ ![]() >1+λ,∴2(x1+λx2)>a(1+λ),
>1+λ,∴2(x1+λx2)>a(1+λ),
∴x1+λx2> ![]() ,∴
,∴ ![]() >1+λ,
>1+λ,
∴ 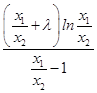 >1+λ,
>1+λ,
∵0<x1<x2 , 令t= ![]() ∈(0,1),∴
∈(0,1),∴ ![]() ,
,
∴(t+λ)lnt﹣(1+λ)(t﹣1)<0,
令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),
则h′(t)=lnt+ ![]() ﹣λ,
﹣λ,
令I(t)=lnt+ ![]() ﹣λ,则I′(t)=
﹣λ,则I′(t)= ![]() =
= ![]() ,(t∈(0,1)),
,(t∈(0,1)),
①当λ≥1时,I′(t)<0,∴h′(t)在(0,1)上单调递减,∴h′(t)>h′(1)=0,
∴h(t)在(0,1)上单调递增,∴h(t)<h(1)=0,符合题意.
②当λ≤0时,I′(t)>0.∴h′(t)在(0,1)上单调递增,∴h′(t)<h′(1)=0,
∴h′(t)在(0,1)上单调递减,∴h(t)>h(1)=0,不符合题意
③当0<λ<1时,I′(t)>0,λ<t<1,∴h′(t)在(λ,1)上单调递增,
∴h′(t)<h′(1)=0,
∴h(t)在(λ,1)上单调递减,∴h(t)>h(1)=0,不符合题意.
综上所述,实数λ的取值范围是[1,+∞).
【解析】(Ⅰ)求出f′(x)=alnx﹣2x,a≠0, ![]() ,令g(x)=
,令g(x)= ![]() ,
, ![]() ,由此利用导数性质能求出实数a的取值范围.(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 , 两式相减,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2
,由此利用导数性质能求出实数a的取值范围.(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 , 两式相减,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2 ![]() ,从而
,从而  >1+λ,令t=
>1+λ,令t= ![]() ∈(0,1),得(t+λ)lnt﹣(1+λ)(t﹣1)<0,令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),则h′(t)=lnt+
∈(0,1),得(t+λ)lnt﹣(1+λ)(t﹣1)<0,令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),则h′(t)=lnt+ ![]() ﹣λ,令I(t)=lnt+
﹣λ,令I(t)=lnt+ ![]() ﹣λ,则I′(t)=
﹣λ,则I′(t)= ![]() =
= ![]() ,(t∈(0,1)),由此利用分类讨论思想,结合导数性质能求出实数λ的取值范围.
,(t∈(0,1)),由此利用分类讨论思想,结合导数性质能求出实数λ的取值范围.
【考点精析】根据题目的已知条件,利用函数的极值与导数和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】九十年代,政府间气候变化专业委员会(IPCC)提供的一项报告指出:使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2浓度增加.据测,1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位。若用函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系,模拟函数可选用二次函数或函数![]() (其中a、b、c为常数).
(其中a、b、c为常数).
(Ⅰ)写出这两个函数的解释式;
(Ⅱ)若知1994年大气中的CO2浓度比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数与1994年的实际数据更接近?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量![]() 单位:吨
单位:吨![]() ,将数据按照
,将数据按照![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
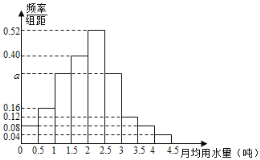
(1)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数![]() 说明理由;
说明理由;
(2)估计居民月均用水量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为了进一步了解学生对智能手机的使用习惯,现在对以上使用智能手机的高中时采用分层抽样的方式,抽取一个容量为![]() 的样本,若抽到的学生中成绩不优秀的比成绩优秀的多
的样本,若抽到的学生中成绩不优秀的比成绩优秀的多![]() 人,求
人,求![]() 的值.
的值.
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωxcosωx﹣ ![]() (ω>0)图象的两条相邻对称轴为
(ω>0)图象的两条相邻对称轴为 ![]() .
.
(1)求函数y=f(x)的对称轴方程;
(2)若函数y=f(x)﹣ ![]() 在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.其图象开口向上,且始终与![]() 轴有两个不同的交点
轴有两个不同的交点
B.无论![]() 取何实数,其图象始终过定点
取何实数,其图象始终过定点![]()
C.其图象对称轴的位置没有确定,但其形状不会因![]() 的取值不同而改变
的取值不同而改变
D.函数的最小值大于![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com