【题目】如果直线y=kx+1与圆x2+y2+kx+my﹣4=0交于M、N两点，且M、N关于直线x+y=0对称，则不等式组：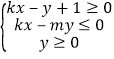
表示的平面区域的面积是（ ）
A.
B.
C.1
D.2
【答案】A
【解析】因为M与N关于x+y=0对称，
直线y=kx+1与直线x+y=0垂直得到k=1，
所以直线MN的方程为y=x+1；
设M（x1 ， y1），N（x2 ， y2），
联立直线与圆的方程得
，
消去y得2x2+（3+m）x+m﹣3=0则x1+x2=﹣
；
由MN中点在直线x+y=0上，代入得
=0即x1+x2+y1+y2=0，
又MN的中点在y=x+1上，得y1=x1+1，y2=x2+1，所以x1+x2=﹣1，
则﹣=﹣1，解得m=﹣1；
所以把k=1，m=﹣1代入不等式组得
，
画出不等式所表示的平面区域如图
△AOB为不等式所表示的平面区域，联立
解得B（﹣
， ），A（﹣1，0），
所以S△AOB=×|﹣1|×|﹣|=
．
故选A
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案科目：高中数学 来源： 题型：
【题目】如图，△ABC的外接圆O的直径为AB，CD⊥平面ABC，BE∥CD．
（1）求证：平面ADC⊥平面BCDE；
（2）试问在线段DE和BC上是否分别存在点M和F，使得平面OMF∥平面ACD？若存在，确定点M和点F的位置；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某中学高中某学科竞赛中，该中学100名考生的参赛成绩统计如图所示．
（1）求这100名考生的竞赛平均成绩（同一组中数据用该组区间中点作代表）；
（2）记70分以上为优秀，70分及以下为合格，结合频率分布直方图完成下表，并判断是否有99%的把握认为该学科竞赛成绩与性别有关？
合格 | 优秀 | 合计 | |
男生 | 18 | ||
女生 | 25 | ||
合计 | 100 |
附：
．
| 0.050 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
上的一动点
到右焦点的最短距离为
，且右焦点到右准线的距离等于短半轴的长．
（1）求椭圆
的方程；
（2）设
是椭圆上关于
轴对称的任意两个不同的点，连接
交椭圆于另一点
，证明直线
与轴相交于定点
；
（3）在（2）的条件下，过点的直线与椭圆交于
两点，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂从一批产品中随机抽取20件进行检测，如图是根据抽样检测后的产品净重（单位：克）数据的频率分布直方图，其中产品净重的范围是[140，200]，样本数据分组为[140，150），[150，160），[160，170），[170，180），[180，190），[190，200]．
（1）求图中a的值；
（2）若频率视为概率，从这批产品中有放回地随机抽取3件，求至少有2件产品的净重在[160，180）中的概率；
（3）若产品净重在[150，190）为合格产品，其余为不合格产品，从这20件抽样产品中任取2件，记X表示选到不合格产品的件数，求X的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列结论错误的是 （ ）
A. 若“
且
”与“
或”均为假命题，则真假.
B. 命题“存在
”的否定是“对任意
”
C. “
”是“
”的充分不必要条件.
D. “若
则a<b”的逆命题为真.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=ax2﹣a﹣lnx，g（x）= 
，其中a∈R，e=2.718…为自然对数的底数．
（1）讨论f（x）的单调性；
（2）证明：当x＞1时，g（x）＞0；
（3）确定a的所有可能取值，使得f（x）＞g（x）在区间（1，+∞）内恒成立．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
