
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=![]() AD,E是线段PD上的点,F是线段AB上的点,
AD,E是线段PD上的点,F是线段AB上的点,
且![]() .
.
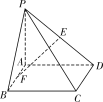
(1)证明:EF∥平面PBC;
(2)是否存在实数λ,使得异面直线EF与CD所成角为60°?若存在,试求出λ的值,若不存在,请说明理由.
【答案】(1)见证明;(2)见解析
【解析】
(1)作EH∥AD交PA于点H,连接HF,结合![]() ,可以证明FH∥PB,从而可以证明平面EFH∥平面PBC,进而得到EF∥平面PBC;(2)异面直线EF与CD所成角为60°,可知
,可以证明FH∥PB,从而可以证明平面EFH∥平面PBC,进而得到EF∥平面PBC;(2)异面直线EF与CD所成角为60°,可知![]() ,则
,则![]() ,再用λ分别表示出
,再用λ分别表示出![]() 与
与![]() ,代入即可求出λ.
,代入即可求出λ.
(1)作EH∥AD交PA于点H,连接HF,
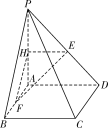
∵EH∥AD,∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴FH∥PB.
又∵EH∥AD,FH∩HE=H,
∴平面EFH∥平面PBC.
∵EF在平面EFH内,∴EF∥平面PBC.
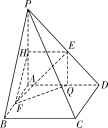
(2)存在实数![]() ,使得异面直线EF与CD所成角为60°.
,使得异面直线EF与CD所成角为60°.
其理由如下:假设存在实数λ,使得异面直线EF与CD所成角为60°,
∵AB∥CD,∴∠AFE为异面直线EF与CD所成角,
∴![]() .
.
过点E作EQ⊥AD交AD于点Q,连接FQ,
∵PA=AD,AB=![]() AD,∴设AD=1,
AD,∴设AD=1,
又∵![]() ,
,
可知![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴存在实数![]() ,使得异面直线EF与CD所成角为60°
,使得异面直线EF与CD所成角为60°


科目:高中数学 来源: 题型:
【题目】排成一排的10名学生生日的月份均不相同.有![]() 名教师,依次挑选这些学生参加
名教师,依次挑选这些学生参加![]() 个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求
个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=4x2-2(t-2)x-2t2-t+1在区间[-1,1]内至少存在一个值m,使得f(m)>0,则实数t的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球赛规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,甲发球得1分的概率为![]() ,乙发球得1分的概率为
,乙发球得1分的概率为![]() ,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: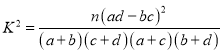 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下说法:
①一年按365天计算,两名学生的生日相同的概率是![]() ;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com