
【题目】在直角坐标系xOy中,![]() 是以PF为底边的等腰三角形,PA平行于x轴,点
是以PF为底边的等腰三角形,PA平行于x轴,点![]() ,且点P在直线
,且点P在直线![]() 上运动.记点A的轨迹为C.
上运动.记点A的轨迹为C.
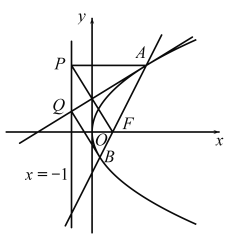
(1)求C的方程.
(2)直线AF与C的另一个交点为B,等腰![]() 底边的中线与直线
底边的中线与直线![]() 的交点为Q,试问
的交点为Q,试问![]() 的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,值为
;(2)存在,值为![]() .
.
【解析】
(1)根据抛物线的定义得轨迹![]() 为抛物线(去除顶点),从而可得其方程;
为抛物线(去除顶点),从而可得其方程;
(2)设直线AB的方程为![]() ,
,![]() ,
,![]() ,直线方程代入抛物线方程整理可得
,直线方程代入抛物线方程整理可得![]() ,由抛物线的焦点弦弦公式求得弦长
,由抛物线的焦点弦弦公式求得弦长![]() ,再求出点
,再求出点![]() 到直线
到直线![]() 的距离,求得三角形面积(表示为
的距离,求得三角形面积(表示为![]() 的函数),由函数性质可得最小值.
的函数),由函数性质可得最小值.
(1)由题意得PA与直线![]() 垂直,且
垂直,且![]() ,
,
故点A到定点![]() 的距离和到直线
的距离和到直线![]() 的距离相等,
的距离相等,
由抛物线的定义可得,C是以![]() 为焦点,
为焦点,
直线![]() 为准线的抛物线(除原点O),
为准线的抛物线(除原点O),
故C的方程为![]() .
.
(2)存在.
设直线AB的方程为![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
则![]() . 又P的坐标为
. 又P的坐标为![]() ,
,
所以PF的中点为![]() ,
,
故![]() 底边的中线所在的直线方程为
底边的中线所在的直线方程为![]() .
.
令![]() ,得
,得 ,
,
故Q的坐标为![]() . 点Q到直线AB的距离
. 点Q到直线AB的距离 ,
,
所以![]() ,
,
故当![]() 时,
时,![]() 取得最小值4.
取得最小值4.


科目:高中数学 来源: 题型:
【题目】在一次篮球投篮测试中,记分规则如下(满分为![]() 分):①每人可投篮
分):①每人可投篮![]() 次,每投中一次记
次,每投中一次记![]() 分;②若连续两次投中加
分;②若连续两次投中加![]() 分,连续三次投中加
分,连续三次投中加![]() 分,连续四次投中加
分,连续四次投中加![]() 分,以此类推,…,七次都投中加
分,以此类推,…,七次都投中加![]() 分.假设某同学每次投中的概率为
分.假设某同学每次投中的概率为![]() ,各次投篮相互独立,则:(1)该同学在测试中得
,各次投篮相互独立,则:(1)该同学在测试中得![]() 分的概率为______;(2)该同学在测试中得
分的概率为______;(2)该同学在测试中得![]() 分的概率为______..
分的概率为______..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一堆100粒的石子进行如下操作:每次任选石子数大于1的一堆任意分成不空的两堆,直到每堆1粒(100堆)为止.证明:
(1)无论如何操作,必有某个时刻存在20堆,其石子总数为60;
(2)可以进行适当地操作使得任何时刻不存在19堆,其石子总数为60.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)点![]() 是该抛物线上任一点,求证:过点
是该抛物线上任一点,求证:过点![]() 的抛物线的切线方程为
的抛物线的切线方程为![]() ;
;
(2)过点![]() 作该抛物线的两条切线,切点分别为
作该抛物线的两条切线,切点分别为![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A.264B.72C.266D.274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司在2020年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利40%,也可能亏损10%,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备据市场调研,投资到该项目上,到年底可能获利50%,可能损失30%,也可能不赔不赚,且这三种情况发生的概率分别为![]() ,
,![]() 和
和![]() .针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
.针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com