
【题目】甲、乙两人分别从4种不同的图书中任选2本阅读,则甲、乙两人选的2本恰好相同的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
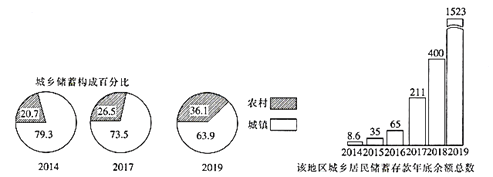
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:存在
满足:存在![]() ,对任意的
,对任意的![]() ,都有
,都有![]() (
(![]() 为常数),则称
为常数),则称![]() 具有性质
具有性质![]()
(1)若无穷数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值
的值
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,并说明理由.
,并说明理由.
(3)设无穷数列![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,其中
,其中![]() 互质,求证:数列
互质,求证:数列![]() 具有性质
具有性质![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),与圆
为参数),与圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,求
两点,求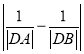 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出春夏两句的有45人,能说出春夏秋三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出第一句“春”或一句也说不出的大约有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R).
R).
(1)当b=﹣1时,函数![]() 有两个极值,求a的取值范围;
有两个极值,求a的取值范围;
(2)当a+b=1时,函数![]() 的最小值为2,求a的值;
的最小值为2,求a的值;
(3)对任意给定的正实数a,b,证明:存在实数![]() ,当
,当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com