

(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长;
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示).
解:(1)正三棱柱ABC—A1B1C1的侧面展开图是一个长为9,宽为4的矩形,其对角线的长为![]()

(2)如图,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连结MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.设PC=x,则P1C=x.
在Rt△MAP1中,由勾股定理得(3+x)2+22=29.
解得x=2,PC=P1C=2.
![]()
(3)如图,连接PP1,则PP1就是平面NMP与平面ABC的交线.
作NH⊥PP1于H,又CC1⊥平面ABC,连结CH,
由三垂线定理得:CH⊥PP1,
∴∠NHC就是平面NMP与平面ABC所成二面角的平面角(锐角).
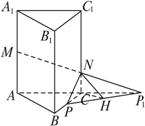
在Rt△PHC中,∵∠PCH=![]() ∠PCP1=60°,
∠PCP1=60°,
∴CH=![]() PC=1.在Rt△NCH中,
PC=1.在Rt△NCH中,
tan∠NHC=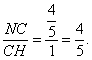
故平面NMP与平面ABC所成二面角(锐角)的大小为arctan![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com