
【题目】假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者.现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以![]() 表示,被捕食者的数量以
表示,被捕食者的数量以![]() 表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
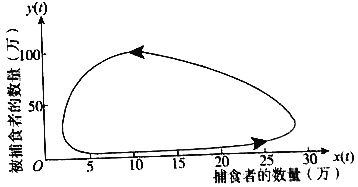
A.若在![]() 、
、![]() 时刻满足:
时刻满足:![]() ,则
,则![]()
B.如果![]() 数量是先上升后下降的,那么
数量是先上升后下降的,那么![]() 的数量一定也是先上升后下降
的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数量与捕食者数量总和达到最大值时,被捕食者的数量也会达到最大值
【答案】C
【解析】
根据图形可判断A选项的正误;根据曲线上半段中![]() 和
和![]() 的变化趋势可判断B选项的正误;根据捕食者和被捕食者的最值情况可判断C选项的正误;取
的变化趋势可判断B选项的正误;根据捕食者和被捕食者的最值情况可判断C选项的正误;取![]() ,
,![]() 可判断D选项的正误.
可判断D选项的正误.
由图可知,曲线中纵坐标相等时横坐标未必相等,故A不正确;
在曲线上半段中观察到![]() 是先上升后下降,而
是先上升后下降,而![]() 是不断变小的,故B不正确;
是不断变小的,故B不正确;
捕食者数量最大时是在图象最右端,最小值是在图象最左端,此时都不是被捕食者的数量的最值处,
同样当被捕食者的数量最大即图象最上端和最小即图象最下端时,也不是捕食者数量取最值的时候,
所以被捕食者数量和捕食者数量不会同时达到最大和最小值,故C正确;
当捕食者数量最大时在图象最右端,![]() ,
,![]() ,
,
此时二者总和![]() ,由图象可知存在点
,由图象可知存在点![]() ,
,![]() ,
,
![]() ,所以并不是被捕食者数量与捕食者数量总和达到最大值时,
,所以并不是被捕食者数量与捕食者数量总和达到最大值时,
被捕食者数量也会达到最大值,故D错误,
故选:C.


科目:高中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
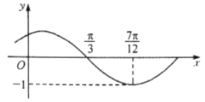
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 上一动点,点
上一动点,点![]() 分别是左、右两个焦点.
分别是左、右两个焦点.![]() 面积的最大值为
面积的最大值为![]() ,且椭圆的长轴长为
,且椭圆的长轴长为![]() .
.
(1)求椭圆的标准方程;
(2)若点![]() ,
,![]() 在椭圆上,已知两点
在椭圆上,已知两点![]() ,
,![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() .求证:
.求证:![]() 的面积
的面积![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com