Question

【题目】在平面直角坐标系中，将曲线：上的点按坐标变换，得到曲线，为与轴负半轴的交点，经过点且倾斜角为的直线与曲线的另一个交点为，与曲线的交点分别为，（点在第二象限）.

（Ⅰ）写出曲线的普通方程及直线的参数方程；

（Ⅱ）求的值.

Answer 1

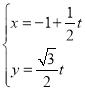【答案】（Ⅰ），（为参数）；（Ⅱ）

【解析】

（Ⅰ）利用伸缩变换公式，把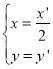代入的方程，化简整理即可；由曲线的方程求出点的坐标，利用倾斜角求出其余弦值和正弦值，代入直线参数方程的标准形式即可求解；

（Ⅱ）利用弦长公式求出,联立直线的参数方程和曲线的方程，利用直线参数方程中参数的几何意义求出，进而求出的值.

（Ⅰ）由题得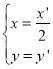代入的方程得

：，即的方程为，

因为曲线：，令，则，

因为为与轴负半轴的交点，所以点，

因为直线的倾斜角为，所以，

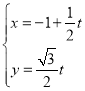所以的参数方程为（为参数）；

（Ⅱ）因为，所以直线的方程为，

因为圆的圆心为，半径为，所以圆心到直线的距离为

，

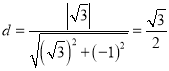由弦长公式可得，，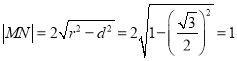

将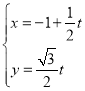（为参数）代入，整理得，

设，为方程的两个根，则，，

∴.