
����Ŀ����ʦ���и���ѧ��ͳ�Ƽס��������༶һģ��ѧ����(����150��),ÿ���༶20��ͬѧ,���мס�����λͬѧ��20�γɼ������о�Ҷͼ��ʾ:
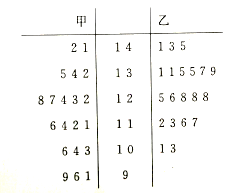
(I)���ݻ�Ҷͼ��ס�����λͬѧ�ɼ�����λ��,������ͬѧ�ijɼ���Ƶ�ʷֲ�ֱ��ͼ���������
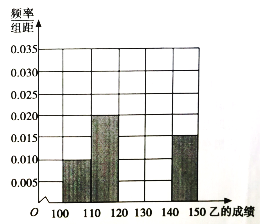
(��)���ݻ�Ҷͼ�Ƚϼ�����λͬѧ��ѧ�ɼ���ƽ��ֵ���ȶ��̶�(��Ҫ����������ֵ���������ۼ���)
(��)�ִӼ�����λͬѧ�IJ�����140�ֵijɼ�������ѡ��2���ɼ������¼�![]() Ϊ������2 ���ɼ��ֱ����ڲ�ͬ��ͬѧ�������¼�
Ϊ������2 ���ɼ��ֱ����ڲ�ͬ��ͬѧ�������¼�![]() �����ĸ���.
�����ĸ���.
���𰸡���I��������.
�����ҵijɼ���ƽ���ֱȼijɼ���ƽ���ָߣ���ͬѧ�ijɼ��ȼ�ͬѧ�ijɼ����ȶ�����.
��III��![]() .
.
����������������I��������λ���Ķ���ɵüס�����λͬѧ�ɼ�����λ��,�ɾ�Ҷͼ�ɵ�Ƶ������Ƶ����Ƶ�ʣ��Ӷ��ɵ������꣬�����ɲ�ȫֱ��ͼ�����Ӿ�Ҷͼ���Կ������ҵijɼ���ƽ���ֱȼijɼ���ƽ���ָߣ���ͬѧ�ijɼ��ȼ�ͬѧ�ijɼ����ȶ���������III�������оٷ���������λͬѧ�IJ�����140�ֵijɼ�������ѡ��2���ɼ��Ļ����¼���![]() ��������2���ɼ�������ͬͬѧ���¼���
��������2���ɼ�������ͬͬѧ���¼���![]() �������ùŵ�����ʹ�ʽ�ɵý��.
�������ùŵ�����ʹ�ʽ�ɵý��.
�������I���ijɼ�����λ����119,�ҵijɼ�����λ����128��
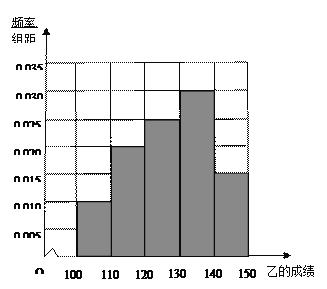
��II��
�Ӿ�Ҷͼ���Կ������ҵijɼ���ƽ���ֱȼijɼ���ƽ���ָߣ���ͬѧ�ijɼ��ȼ�ͬѧ�ijɼ����ȶ����� . ��III����ͬѧ�IJ�����140�ֵijɼ���2����Ϊa,b,��ͬѧ�IJ�����140�ֵijɼ���3������Ϊc,d,e
�ִӼ�����λͬѧ�IJ�����140�ֵijɼ�������ѡ��2���ɼ��У�(a,b),(a,c)(a,d)(a,e)(b,c)(b,d)(b,e)(c,d)(c,e)(d,e)��10�֣�
����2���ɼ�������ͬͬѧ������У� (a,c)(a,d)(a,e)(b,c)(b,d)(b,e)��6��
����¼�A�����ĸ���P(A)=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���ѧ���Խ�ͨ��ȫ֪ʶ�������������ũ����ѧ�ͳ�����ѧ��ѡȡ100��ͬѧ���н�ͨ��ȫ֪ʶ����.��ͼ1��ͼ2�ֱ��Ƕ�ũ����ѧ�ͳ�����ѧ�μӾ�����ѧ���ɼ���![]() ��
��![]() ��
��![]() ��
��![]() ���飬�õ���Ƶ�ʷֲ�ֱ��ͼ.
���飬�õ���Ƶ�ʷֲ�ֱ��ͼ.
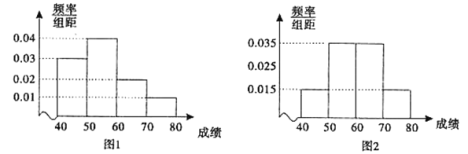
���ֱ����μ����֪ʶ������ũ����ѧ�ͳ�����ѧ��ƽ���ɼ���
�����������![]() �����������ش��Ƿ���
�����������ش��Ƿ���![]() �İ�����Ϊ��ũ����ѧ�ͳ�����ѧ��ѧ���Խ�ͨ��ȫ֪ʶ������������������족��
�İ�����Ϊ��ũ����ѧ�ͳ�����ѧ��ѧ���Խ�ͨ��ȫ֪ʶ������������������족��
�ɼ�С��60������ | �ɼ���С��60������ | �ϼ� | |
ũ����ѧ | |||
������ѧ | |||
�ϼ� |
����![]()
�ٽ�ֵ����
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ,���ҽ���ֱ�Ϊ
,���ҽ���ֱ�Ϊ![]() ��
��![]() ��
��![]()
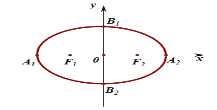
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�����ҽ���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ���㣬��̽����
���㣬��̽����![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() Ϊ��ֵ�������������
Ϊ��ֵ�������������![]() �����꣬����������˵�����ɣ�
�����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ������
������![]() ��
��![]() �������߷���Ϊ
�������߷���Ϊ![]() .
.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��3����![]() �������
�������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ�У���ԭ��Ϊ���㣬��![]() ��ķǸ�����Ϊ������ȡ��ͬ�ĵ�λ���Ƚ���������ϵ������
��ķǸ�����Ϊ������ȡ��ͬ�ĵ�λ���Ƚ���������ϵ������![]() �ļ����귽��Ϊ��
�ļ����귽��Ϊ��![]() .
.
��1��������![]() ����������
����������![]() ��
��![]() ��������������
Ϊ��������������![]() ��ֱ�����귽�̺�����
��ֱ�����귽�̺�����![]() ����ͨ���̣�
����ͨ���̣�
��2��������![]() ����������
����������![]() ��
��![]() ��������
��������![]() ��������
��������![]() ������
������![]() ����ֱ�Ϊ
����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ���������һ���д���������ڸ��ݽ�����Ĺ�����������������ȷ���˴ι���֧��������֧��x����Ԫ����������y����̨�����������£�

��1���������Իع�ģ�����y��x�Ĺ�ϵ�����y����x�����Իع鷽�̣�����![]() ���ο����̣��ع�ֱ��
���ο����̣��ع�ֱ�� ��
��![]() ��
��
��2������ģ��![]() ���y��x�Ĺ�ϵ���ɵûع鷽��
���y��x�Ĺ�ϵ���ɵûع鷽��![]() �����������Իع�ģ�ͺ�ģ�͵�
�����������Իع�ģ�ͺ�ģ�͵�![]() �ֱ�ԼΪ0.75��0.88������
�ֱ�ԼΪ0.75��0.88������![]() ˵��ѡ���ĸ��ع�ģ���ã�
˵��ѡ���ĸ��ع�ģ���ã�
��3����֪����z��x��y�Ĺ�ϵΪz��200y��x�����ݣ�2���Ľ���ش𣺵�����x��20ʱ���������������Ԥ��ֵ�Ƕ��٣�����ȷ��0.01���ο����ݣ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ������Ϊ
������Ϊ![]() ����
����![]() Ϊ��Բ��һ�㣬
Ϊ��Բ��һ�㣬![]() ��
��![]() �����Ϊ
�����Ϊ![]() .
.
��1������Բ�ı����̣�
��2�����![]() Ϊ��Բ���϶��㣬����Բ��һ��
Ϊ��Բ���϶��㣬����Բ��һ��![]() ��ֱ��
��ֱ��![]() ����Բ��
����Բ��![]() ���㣬��
���㣬��![]() ��
��![]() �������Ϊ
�������Ϊ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() ��
��![]() ��������
��������![]() ��
��![]() ����ʹ��
����ʹ��![]() ����P�����õ�����
����P�����õ�����![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() .
.


��1����![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ����˵����Ľ��ۣ�
����˵����Ľ��ۣ�
��2����֤��![]() ƽ��
ƽ��![]() ��
��
��3�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B��C��������![]() ��
��
��1����֤��A��B��C���㹲�ߣ�
��2����A��1��cosx����B��1+sinx��cosx������x��[0�� ![]() ]������f��x��=
]������f��x��=![]() ��2m+
��2m+![]() ��|
��|![]() |+m2����СֵΪ5����ʵ��m��ֵ��
|+m2����СֵΪ5����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com