
【题目】选修4-4,坐标系与参数方程
已知在平面直角坐标系xOy中,椭圆C的方程为![]() ,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线
,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设M(x,y)为椭圆C上任意一点,求|![]() x+y﹣1|的最大值.
x+y﹣1|的最大值.
【答案】(1)![]() (2)9
(2)9
【解析】试题分析:(1)根据![]() 将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|
将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|![]() x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
试题解析:(1)根据题意,椭圆C的方程为![]() +
+![]() =1,
=1,
则其参数方程为![]() ,(α为参数);
,(α为参数);
直线l的极坐标方程为ρsin(θ+![]() )=3,变形可得ρsinθcos
)=3,变形可得ρsinθcos![]() +ρcosθsin
+ρcosθsin![]() =3,
=3,
即![]() ρsinθ+
ρsinθ+![]() ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得
ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得![]() x+y﹣6=0,
x+y﹣6=0,
即直线l的普通方程为![]() x+y﹣6=0;
x+y﹣6=0;
(2)根据题意,M(x,y)为椭圆一点,则设M(2cosθ,4sinθ),
|2![]() x+y﹣1|=|4
x+y﹣1|=|4![]() cosθ+4sinθ﹣1|=|8sin(θ+
cosθ+4sinθ﹣1|=|8sin(θ+![]() )﹣1|,
)﹣1|,
分析可得,当sin(θ+![]() )=﹣1时,|2
)=﹣1时,|2![]() x+y﹣1|取得最大值9.
x+y﹣1|取得最大值9.


科目:高中数学 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
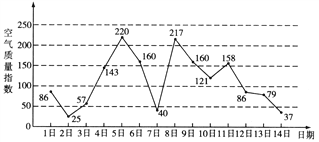
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() .
.

(1)证明:![]() ;
;
(2)设![]() 是线段
是线段![]() 上的动点,是否存在这样的点
上的动点,是否存在这样的点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,如果存在,求出
,如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且![]() ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得![]() ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作![]() 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:![]() 为定值.
为定值.![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )
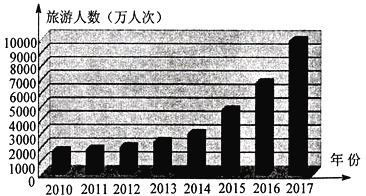
A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届宁夏育才中学高三上学期期末】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
(1)根据频率分布直方图计算图中各小长方形的宽度;

(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
![]()
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.
参考公式: 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com