
| A. | $\frac{1}{x+y}$≤$\frac{1}{4}$ | B. | $\frac{1}{x}$+$\frac{1}{y}$≤1 | C. | $\sqrt{xy}$≥2 | D. | $\frac{1}{xy}$≥$\frac{1}{4}$ |
分析 由 x>0,y>0.且 x+y≤4,利用不等式的性质进行判断.
解答 解:若 x>0,y>0.且 x+y≤4,则$\frac{1}{x+y}$≥$\frac{1}{4}$,故A错误;
$\frac{2}{\frac{1}{x}+\frac{1}{y}}$≤$\frac{x+y}{2}$≤2,当且仅当x=y=2时成立,则$\frac{1}{x}$+$\frac{1}{y}$≥1,故B错误;
4≥x+y≥2$\sqrt{xy}$,当且仅当x=y=2时取“=”,故$\sqrt{xy}$≤2,故C错误;
$\sqrt{xy}$≤2,得:0<xy≤4,即$\frac{1}{xy}$≥$\frac{1}{4}$,故D正确,
故答案选:D.
点评 本题考查基本不等式的性质及应用,熟练掌握基本不等式的性质是解题的关键,属于基础题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
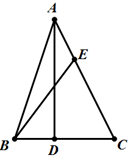 如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6
如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com